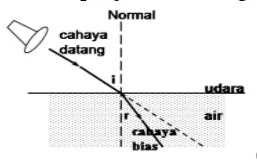
Misalnya, cahaya dari udara memasuki air; karena udara dan air adalah dua medium yang berbeda maka arah rambat cahaya pada medium tersebut akan berbeda. Bila seberkas sinar masuk dari medium yang index biasnya lebih besar kedalam medium yang index biasnya lebih kecil, maka sudut biasnya lebih besar daripada sudut datangnya (sinar bias menjauhi garis normal).
PEMBIASAN CAHAYA
Hukum Snellius adalah rumus matematika yang memberikan hubungan antara sudut datang dan sudut bias pada cahaya atau gelombang lainnya yang melalui bidang batas antara dua medium isotropik berbeda, seperti udara dan gelas. Hukum Snellius menyebutkan bahwa perbandingan sinus sudut datang dan sudut bias adalah konstan, yang tergantung pada medium.A. Kaca Plan Paralel
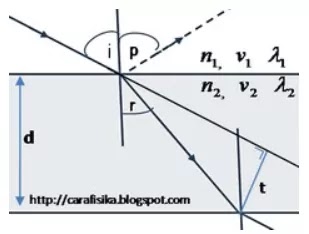
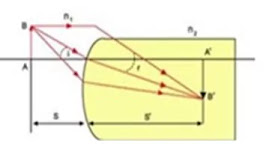
Kaca plan paralel atau balok kaca adalah keping kaca tiga dimensi yang kedua sisinya dibuat sejajar Perumusan matematis hukum Snellius adalah untuk Kaca Plan
Pararel: \[\frac{\sin i}{\sin r} = \frac{v_1}{v_2} =\frac{\lambda _1}{\lambda _2}= \frac{n_2}{n_1}={n_{21}} = \frac{1}{n_{21}} \] dimana
a.mendekati garis normal
- $n_{21}$ adalah indeks bias relatif medium kedua terhadap medium pertama, dan
$n_{12}$ adalah indeks bias relatif medium pertama terhadap medium kedua.
a.mendekati garis normal
Cahaya dibiaskan mendekati garis normal jika cahaya merambat dari medium optik kurang rapat ke medium optik lebih rapat, contohnya cahaya merambat dari udara ke dalam air.
b. menjauhi garis normal
Cahaya dibiaskan menjauhi garis normal jika cahaya merambat dari medium optik
lebih rapat ke medium optik kurang rapat, contohnya cahaya merambat dari dalam air ke udara.
Pergeseran Sinar pada plan pararel\[t=d\frac{\sin (i – r)}{\cos r}\]d = tebal balok kaca, (cm) dan t = pergeseran cahaya, (cm)
Pembiasan bidang pembias I (di titik A) \[\frac{\sin i_{1}}{\sin r_{1}} = \frac{n_2}{n_1}\]\[r_{1}+i_{2}=\beta\] Pembiasan bidang pembias I (di titik A) \[\frac{\sin i_{2}}{\sin r_{2}} = \frac {n_1}{n_2}\] \[i_{1}+r_{2}=\beta + D \]
Keterangan:
1. Bila sudut pembias lebihFisika dari 15° \[\small n_{2}= \frac{n_{1}\sin \frac{1}{2}\left ( \beta +D_{min} \right )}{\sin \frac{1}{2}\beta }\]Keterangan :
Penyelesaian Fisika:
Bayangan sejati dihasilkan saat benda berada pada jarak lebih besar dari fokus lensa (s>f). Saat benda digerakkan mendekati lensa, maka bayangan bergerak menjauhi lensa dengan kecepatan yang lebih kecil dari kecepatan bendanya.
Pergeseran Sinar pada plan pararel\[t=d\frac{\sin (i – r)}{\cos r}\]d = tebal balok kaca, (cm) dan t = pergeseran cahaya, (cm)
B. Pembiasan Pada Prisma
Prisma adalah zat bening yang dibatasi oleh dua bidang datar. Apabila seberkas sinar datang pada salah satu bidang prisma yang kemudian disebut sebagai bidang pembias I, akan dibiaskan mendekati garis normal. Sampai pada bidang pembias II, berkas sinar tersebut akan dibiaskan menjauhi garis normal.- ß = sudut puncak atau sudut pembias prisma
$i_{1}$ = sudut datang pada bidang batas pertama
$r_{1}$ = sudut bias bidang batas pertama
$i_{2}$ = sudut datang bidang batas kedua
$r_{2} $= sudut bias bidang batas kedua
D = sudut deviasi
Jila $i_{1}=r_{2}$ dan $r_{1}=i_{2}$ maka deviasi adalah bernilai minimum.
1. Bila sudut pembias lebihFisika dari 15° \[\small n_{2}= \frac{n_{1}\sin \frac{1}{2}\left ( \beta +D_{min} \right )}{\sin \frac{1}{2}\beta }\]Keterangan :
- $n_{1}$ = indeks bias medium
$n_{2}$ = indeks bias prisma Dm = deviasi minimum
ß = sudut pembias prisma
- $D_{min}$ = deviasi minimum untuk b = 15°
$n_{2-1}$ = indeks bias relatif prisma terhadap medium
ß = sudut pembias prisma
c. Pembiasan pada bidang lengkung
\[\frac{n_{1}}{S}+\frac{n_{2}}{S^{'}}=\frac{n_{2}-n_{1}}{R}\]Keterangan:- $n_{1}$ = indeks bias medium di sekitar permukaan lengkung ;
$n_{2}$ = indeks bias permukaan lengkung
S = jarak benda ;
$S^{‘}$ = jarak bayangan
R = jari-jari kelengkungan permukaan lengkung
D. Soal dan Penyelesaian
Soal 1. Jika sebuah benda di depan lensa positif digerakkan mendekati lensa, bayangan sejati akan ….Penyelesaian Fisika:
Bayangan sejati dihasilkan saat benda berada pada jarak lebih besar dari fokus lensa (s>f). Saat benda digerakkan mendekati lensa, maka bayangan bergerak menjauhi lensa dengan kecepatan yang lebih kecil dari kecepatan bendanya.
Soal 2. Sebuah prisma kaca dengan sudut pembias $\small 60^{o}$ berada di ruangan terbuka. Pada prisma itu didatangkan seberkas sinar dengan sudut datang $\small 45^{o}$ . Jika terjadi deviasi minimum, berapa indeks bias prima tersebut?
Penyelesaian Fisika:
a. di udara:\[\begin{align*} D_{min}&=\left ( \frac {n_{p}}{n_{m}} - 1 \right )\beta\\ D_{min}&=\left ( \frac {1,5}{1} - 1 \right )10^{o}=5^{o}\end{align*}\] b. di air:\[\begin{align*} D_{min}&=\left ( \frac {n_{p}}{n_{m}} - 1 \right )\\ D_{min}&=\left ( \frac {1,5}{\frac {4}{3}} - 1 \right )10^{o}=1,25^{o}\end{align*}\]
Penyelesaian Fisika:
\[\begin{align*} 2i &=\beta +D_{min}\\2x45&=60+D_{min}\\\\ D_{min}&=30\\ n_{p}&= \frac{n_{u}\sin \frac{1}{2}\left ( \beta +D_{min} \right )}{\sin \frac{1}{2}\beta }\\ n_{p}&= \frac{1\sin \frac{1}{2}\left ( 60 +30 \right )}{\sin \frac{1}{2}60 }\\ n_{p}&= \frac{sin 45}{\sin 30 }\\ n_{p}&= \sqrt{2}\end{align*}\] Soal 3. Pada percobaan pembiasan cahaya dengan kaca plan pararel, seberkas sinar masuk dengan sudut datang $\small 60^{o}$ dan dibiaskan dengan sudut $\small 30^{o}$. Jika ketebalan kaca plan pararel adalah $10\sqrt {3}$ cm, berapakah pergeseran sinar keluar terhadap sinar masuk pada percobaan tersebut.
Penyelesaian Fisika:\[\begin{align*} t&=d\frac{\sin (i – r)}{\cos r}\\ t&=10\sqrt {3}\frac{\sin (60 – 30)}{\cos 30}\\ t&=10\sqrt {3}\frac{\sin 30}{\cos 30}\\ t&=10\;cm\end{align*}\] Soal 4. Sebuah prisma dengan sudut pembias $\small 10^{o}$ dan index biasnya 1,5. Deviasi minimum prisma tersebut bila berada di udara dan bila berada di dalam air yang berindex bias 4/3.Penyelesaian Fisika:
a. di udara:\[\begin{align*} D_{min}&=\left ( \frac {n_{p}}{n_{m}} - 1 \right )\beta\\ D_{min}&=\left ( \frac {1,5}{1} - 1 \right )10^{o}=5^{o}\end{align*}\] b. di air:\[\begin{align*} D_{min}&=\left ( \frac {n_{p}}{n_{m}} - 1 \right )\\ D_{min}&=\left ( \frac {1,5}{\frac {4}{3}} - 1 \right )10^{o}=1,25^{o}\end{align*}\]
