GELOMBANG STASIONER UJUNG BEBAS DAN UJUNG TERIKAT

Teman-teman mencari materi gelombang stasioner? ini dia materi gelombang stasioner; Persamaan atau rumus gelombang stasioner, soal jawab gelombang stasioner, baik gelombang stasioner ujung terikat maupun gelombang stasioner ujung bebas.

Soal Dan Pemyelesaian Fisika SMA - Gelombang stasioner terjadi jika dua gelombang yang mempunyai frekuensi dan amplitudo sama bertemu dalam arah yang berlawanan.

Gelombang stasioner memiliki ciri-ciri, yaitu terdiri atas simpul dan perut. Simpul yaitu tempat kedudukan titik yang mempunyai amplitudo minimal (nol), sedangkan perut yaitu tempat kedudukan titik-titik yang mempunyai amplitudo maksimum pada gelombang tersebut.

Gelombang stasioner dapat dibedakan menjadi dua, yaitu Gelombang stasioner yang terjadi pada ujung pemantul bebas dan gelombang stasioner yang terjadi pada ujung pemantul tetap.

PERSAMAAN GELOMBANG STASIONER UJUNG TERIKAT

---

Seutas tali diikatkan salah satu ujungnya pada satu tiang sementara ujung lainnya kita biarkan, bila ujung yang bebasnya digetarkan keatas dan kebawah berulang – ulang maka gelombang akan merambat dari ujung yang bebas menuju ujung yang terikat, gelombang ini disebut sebagai gelombang datang. Ketika gelombang datang tiba di ujung yang terikat maka gelombang ini akan dipantulkan sehingga terjadi interferensi gelombang. 

pada titik Q gelombang datang memiliki persamaan \begin{align*}y_{1}&= A sin\left ( \omega t - kx \right )\end{align*} dan persamaan gelombang pantul yang sampai di titik C dinyatakan; \begin{align*} y_{2}&= A sin\left ( \omega t + kx \right )\end{align*} maka persamaan gelombang stasioner di titik O dinyatakan sebagai $ y_{1}+y_{2}$ sehingga untuk hasil interferensi gelombang datang dan gelombang pantul di titik O yang berjarak x dari ujung terikat P adalah sebagai berikut:
$\begin{align*}y&=y_{1}+y_{2}\\y&= A sin\left ( \omega t - kx \right )+A sin\left ( \omega t + kx \right )\end{align*}$ 

Dengan menggunakan aturan sinus:

$\small \begin{align*}\sin A+\sin B = 2\sin\frac{1}{2}(A+B).\cos\frac{1}2{(A-B)}\end{align*}$

Persamaan simpangan menjadi: 

$\begin{align*}y= 2 A \sin{(kx)}. \cos{(\omega t})\end{align*}$

Keterangan :

• A = amplitude gelombang datang atau pantul (m)
• $ k=\frac{2\pi }{\lambda}$ bilangan gelombang
• $ \omega ={2\pi }{f}=\frac{2\pi }{T}$
• $l$ = panjang tali (m)
• $x$ = letak titik dari ujung terikat (m)
• $\lambda$ = panjang gelombang (m)
• $t$ = waktu sesaat (s)
• $ Ap = 2 A sin kx$ = amplitudo gelombang stasioner (AP)

Tempat simpul (S) dari ujung pemantulan: 

$S_{n}=(n-1)\frac{1}{2}\lambda$

dengan n = 1, 2, 3,… sehingga 

$ S_{n}=0,\frac{1}{2}\lambda ,\frac{3}{2}\lambda ,\frac{5}{2}\lambda ,\frac{7}{2}\lambda $ dst
Tempat perut (p) dari ujung pemantulan: 

$P_{n}=(2n-1)\frac{1}{4}\lambda$

dengan n      = 1, 2, 3,… sehingga 

$ P_{n}=\frac{1}{4}\lambda ,\frac{3}{4}\lambda ,\frac{5}{4}\lambda ,\frac{7}{4}\lambda $ dan seterusnya.

PERSAMAAN GELOMBANG STASIONER UJUNG BEBAS

---

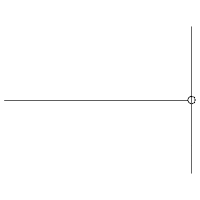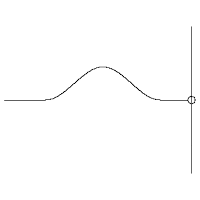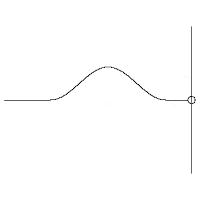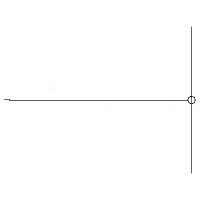Jika kita perhatikan gambar pemantulan gelombang di atas , gelombang yang terbentuk adalah gelombang transversal yang memiliki bagian – bagian diantaranya perut dan simpul gelombang. Perut gelombang terjadi saat amplitudonya maksimum sedangkan simpul gelombang terjadi saat amplitudonya minimum. Dengan demikian kita akan dapat mencari letak titik yang merupakan tempat terjadinya perut atau simpul gelombang. 
Persamaan simpangan:\[  y= 2 A cos{(kx)}. sin{(\omega t})\]
Tempat Simpul (S) dari ujung pemantulan:\[  S_{n}=(2n-1)\frac{1}{4}\lambda\] dengan n=1,2,3,… sehingga 

$ S_{n}=\frac{1}{4}\lambda ,\frac{3}{4}\lambda ,\frac{5}{4}\lambda ,\frac{7}{4}\lambda ,$ dan seterusnya.
Tempat Perut (P) dari ujung pemantulan:

$ P_{n}=(n-1)\frac{1}{2}\lambda$ dengan n=1,2,3,… 
sehingga $ P_{n}=0,\frac{1}{2}\lambda ,\frac{3}{2}\lambda ,\frac{5}{2}\lambda ,\frac{7}{2}\lambda ,$ dst

SOAL DAN PENYELESAIAN GELOMBANG STASIONER UJUNG BEBAS DAN UJUNG TERIKAT

---

Seutas tali panjangnya 5 m dengan ujung ikatannya dapat bergerak dan ujung lainnya digetarkan dengan frekuensi 8 Hz sehingga gelombang merambat dengan kelajuan 3 m$s^{-1}$. Jika diketahui amplitude gelombang 10 cm, tentukanlah:

1. Persamaan simpangan superposisi gelombang di titik P yang berjarak 1 meter dari ujung pemantulan.
2. Amplitude superposisi gelombang di titik P; dan
3. Letak perut gelombang diukur dari ujung pemantulan.

---

Jawaban Fisika dari Pak Dimpun:
$\begin{align*}k &= \frac{2\pi }{\lambda }=\frac{2\pi }{3/8}\\k&={\frac{16\pi}{3}} \\ \omega &= 2\pi f= 2\pi (8) \\\omega &= 16\pi \textrm{ rad/s}\end{align*}$
1. Persamaan simpangan di titik P, satu meter dari ujung pemantulan. 

$\small \begin{align*} y &= 2 A \cos (kx)\sin \left ( \omega t-\frac{2\pi l}{\lambda } \right ) \\y&= 2 (0,1) \cos (\frac{16\pi}{3} (1))\sin \left ( 16\pi t-\frac{2\pi (5)}{3/8} \right )\\ y &= 0,2 \cos (\frac{16\pi}{3} )\sin \left ( 16\pi t-\frac{80\pi }{3 } \right ) \\ y &= 0,2 \cos 2\pi (\frac{8}{3} )\sin 2\pi \left ( 8 t-\frac{40 }{3 } \right )\end{align*}$

---

2. Amplitudo superposisi gelombang di titik P ( x = 1 m ).
$\begin{align*}y &= 0,2 \cos 2\pi (\frac{8}{3} )\\y&= 0,2 \cos 2\pi (\frac{4}{3} )=- 0,1 m\end{align*}$ 

tanda (–) menunjukkan di titik P simpangannya ke bawah

---

3. Letak perut gelombang dari ujung pemantulan.
$ x = \left (\frac{n+1}{2} \right ) \lambda$, dengan n = 1,2,3…
$ x = 0, \frac{3}{16}m,\frac{6}{16}m,\frac{9}{16}m....$ 

---

4. Soal yang anda cari mungkin di sini:

• SOAL DAN PENYELESAIAN GELOMBANG STASIONER UJUNG BEBAS DAN TERIKAT 
• Silahkan lihat post kami yang lain melalui daftar isi blog di sini...