Soal dan Penyelesaian Fisika - Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang.
 Vektor yang dipergunakan untuk menentukan posisi disebut adalah VEKTOR POSISI yang ditulis dalam Vektor satuan.
Vektor yang dipergunakan untuk menentukan posisi disebut adalah VEKTOR POSISI yang ditulis dalam Vektor satuan.VEKTOR SATUAN.
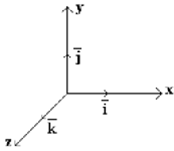
$\left | \bar{i} \right |=\left | \bar{j} \right |=\left | \bar{k} \right |=1$
dimana:
$\left | \bar{i} \right |$ vektor satuan pada sumbu x.
$\left | \bar{j} \right |$ vektor satuan pada sumbu y.
$\left | \bar{k} \right |$ vektor satuan pada sumbu z.
POSISI TITIK MATERI PADA SUATU BIDANG DATAR.
Posisi titik materi ini dapat dinyatakan dengan :
$\bar{r}=x_{\bar{i}}+y_{\bar{j}}$
Panjang r ditulis: $\left | \bar{r} \right |=\sqrt{x^{2}+y^{2}}$
Contoh : $\bar{r}=5i+3j$
Panjang $\left | \bar{r} \right |=\sqrt{5^{2}+3^{2}}=\sqrt{34}$
POSISI TITIK MATERI PADA SUATU RUANG.
Posisi titik materi ini dapat dinyatakan dengan : $\bar{r}=x_{\bar{i}}+y_{\bar{j}}+z_{\bar{k}}$
Contoh : $\bar{r}=4i+3j+2z$
Panjang $\left | \bar{r} \right |=\sqrt{4^{2}+3^{2}+2^{2}}=\sqrt{29}$ satuan
KECEPATAN SUATU TITIK MATERI.
Gerakan titik materi secara keseluruhan dapat diamati jika posisinya setiap saat diketahui. Seberapa cepat letak titik materi itu berubah setiap saat disebut : KECEPATAN .
PERHATIKAN Titik materi yang bergerak dari A yang posisinya posisinya $\bar{r_1}$ pada saat $t_{1}$, ke titik B yang posisinya $\bar{r_1}$ pada saat $t_{2}.$

Vektor perpindahannya $\Delta \bar{r}=\bar{r_{2}}-\bar{r_{1}}$ dan selang waktu yang dipergunakan titik materi untuk bergerak dari A ke B adalah $\Delta t = t_2-t_1$
Kecepatan rata-rata didefinisikan : $\bar{v}=\frac{\Lambda r}{\Delta t}=\frac{\bar{1_{2}}-\bar{r_{1}}}{t_2-t_1}$
Pada persamaan di atas tampak bahwa kecepatan rata-rata tidak tergantung pada lintasan titik materi, tetapi tergantung dari posisi awal $\bar{r_1}$ dan posisi akhir $\bar{r_2}$. Jika ingin diketahui kecepatan titik materi pada suatu saat misal saat titik materi berada di antara A dan B, digunakan kecepatan sesaat.
Kecepatan sesaat didefinisikan : \[\bar{v}=\lim _{\Delta {t} \to 0 } \frac{\Delta r}{\Delta t}\] Kecepatan sesaat merupakan turunan pertama dari posisi terhadap waktu (t) , Secara matematis ditulis sebagai :\[\bar{v}=\frac{d\bar{r}}{dt}\] Besarnya kecepatan disebut dengan laju
Laju didefinisikan sebagai :\[\left |\bar{v} \right |=\left |\frac{d\bar{r}}{dt} \right |\] Laju dapat pula berarti panjang lintasan dibagi waktu yang bersangkutan.
Nilai dari komponen kecepatan sesaat dari suatu titik materi dapat dilihat dari kemiringan grafik yang dibentuk oleh komponen posisi (r) terhadap waktu (t).

Persamaan kecepatan sesaat dari grafik di samping di dapat :
$v_1=\tan \alpha _1$ dan $ v_2=\tan \alpha_2$
Makin besar derajat kemiringannya makin besar pula harga kecepatannya. Posisi dari suatu titik materi yang bergerak merupakan fungsi waktu, oleh karena itu, vektor posisi$\bar{r}$ dapat ditulis sebagai $\bar{r}=\bar{r_{(t)}}$ artinya $\bar{r}$ adalah fungsi waktu t
Kecepatan titik materi pada sebuah bidang datar/ruang dapat ditulis : \[v_x=\frac{dx}{dt}; v_y=\frac{dy}{dt}; v_z=\frac{dz}{dt}\] X, Y, Z merupakan fungsi dari waktu.
Sebaliknya untuk menentukan posisi titik materi jika diketahui fungsi kecepatannya maka dapat diselesaikan dengan INTEGRAL ( kebalikan dari deferensial ). \[v_{(t)}=\frac{dx_{(t)}}{dt}\]\[ dx_{(t)}=v_{(t)}dt \]\[\int dx_{(t)}=\int v_{(t)}dt\]\[ x_{(t)}=\int v_{(t)}dt\] Contoh :
$v_{(t)} = 2t + 5$ m/det
maka persamaan posisi titik materi tersebut adalah: $r = \int vdt\\r=\int{(2t + 5)}dt \\r= 3t^{2}+5t+c$ Harga c dicari dengan suatu syarat batas tertentu, misalnya : t = 0 nilai $r_{(t)}$ = 0 maka harga c dapat dihitung; c = 0
PERCEPATAN
Kecepatan titik materi dapat berubah-ubah setiap saat baik besar, atau arah, ataupun kedua-duanya yang disebabkan oleh karena adanya percepatan yang dialami oleh titik materi tersebut. Percepatan rata-rata didefinisikan sebagai: \[\bar{a}=\frac{\Delta \bar{v}}{\Delta t}=\frac{\bar{v}_2-\bar{v_1}}{{{t}_2-{t_1}}}\] percepatan sesaatnya \[\bar{a}=\lim _{\Delta {t} \to 0 } \frac{\Delta v}{\Delta t}=\frac{d\bar{v}}{dt}\] \[\bar{a}=\frac{d\bar{v}}{dt}=\frac{d({d\bar{r}})}{dt(t)}=\frac{d^{2}\bar r}{d t^{2}}\] Percepatan merupakan turunan pertama dari kecepatan terhadap waktu (t) atau turunan kedua dari posisi terhadap waktu (t).
Kecepatan sesaat dari suatu titik materi dapat dilihat dari kemiringan komponen grafik kecepatan (v) terhadap waktu (t).
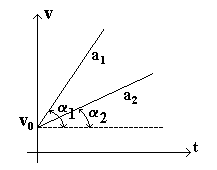
dari grafik di samping besar percepatan sesaat :
$a_1=\tan \alpha _1\\ a_2=\tan \alpha_2$
Percepatan dalam arah masing-masing sumbu dalam bidang/ruang dapat dituliskan sebagai : \[\bar{a_{x}}=\frac{d^{2}r_{\bar x}}{d t^{2}}\\\\ \bar{a_{y}}=\frac{d^{2} r_{\bar y}}{d t^{2}} \\\\ \bar{a_{z}}=\frac{d^{2}r_{\bar z}}{d t^{2}}\] Sebaliknya untuk menentukan kecepatan dari grafik fungsi percepatan terhadap waktu dengan cara mengintegralkan :\[\bar{v}_{(t)}=\bar{v}_o+\int_{o}^{t} \bar a{_{(t)}}dt\]
KESIMPULAN :
Posisi titik materi, kecepatan dan percepatan merupakan besaran vektor, sehingga dapat dinyatakan dengan VEKTOR SATUAN.
POSISI:
\[\bar{r}=x_{\bar{i}}+y_{\bar{j}}+z_{\bar{k}}\]KECEPATAN:
\[\bar{v}={v}_{x}{\bar{i}}+{v}_{y}{\bar{j}}+{v}_{z}{\bar{k}}\] \[\bar{v}=\frac{dx}{dt}\bar{i}+\frac{dy}{dt}\bar{j}+\frac{dz}{dt}\bar{k}\]PERCEPATAN:
\[\bar{a}={a}_{x}{\bar{i}}+{a}_{y}{\bar{j}}+{a}_{z}{\bar{k}}\] \[\bar{a}=\frac{dv_x}{dt}\bar{i}+\frac{dv_y}{dt}\bar{j}+\frac{dv_z}{dt}\bar{k}\] \[\bar{a}=\frac{d^{2}{x}}{d t^{2}}\bar{i}+\frac{d^{2}{y}}{d t^{2}}\bar{j}+\frac{d^{2}{z}}{d t^{2}}\bar{k}\]Lanjut ke:
CONTOH SOAL DAN PENYELESAIAN VEKTOR POSISI