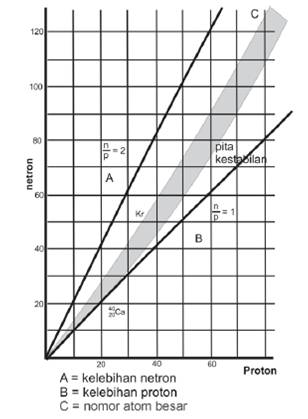
A. Pita kestabilan
Dalam pita kestabilan, ditemukan bahwa kestabilan suatu inti atom ditentukan oleh perbandingan jumlah neutron dan proton. Plot jumlah neutron terhadap jumlah proton dari semua isotop yang sudah dikenal, baik isotop stabil maupun isotop radioaktif disebut peta isotop. Sementara, pita kestabilan adalah isotop-isotop stabil yang terletak dalam suatu daerah berbentuk pita.Dalam kestabilan inti radioaktif, terdapat 3 jenis nuklida:
- Nuklida ringan (Z ≤ 20) ; Nuklida ini mempunyai jumlah proton kurang dari 20, inti stabil jika n = Z atau n/Z = 1. Contoh: 5B10, 7N14, 10Ne200
- Nuklida sedang (Z antara 21-83); Nuklida ini mempunyai jumlah proton antara 20 sampai 83, inti stabil jika n/Z = 1,6. Contoh: 45Rh103, 83Bi209
- Nuklida berat (Z > 83); Nuklida ini dimulai pada unsur yang punya nomor atom (proton) dari 84 hingga seterusnya, tidak ada yang stabil sehingga radioaktif. Contoh: seluruh deret aktinida dan sebagian deret lantanida bersifat nuklida berat
B. Letak Nuklida Dalam Pita Kestabilan
Suatu nuklida bisa memiliki proton > neutron, begitu juga sebaliknya, nuklida yang tidak stabil terbagi atas 3 jenis:1. Nuklida-nuklida di atas pita kestabilan
Syaratnya: jumlah neutron (n) > proton (p), dan untuk mencapai kestabilan harus mengurangi jumlah neutronnya melalui:
a) Memancarkan sinar beta
Akibat memancarkan sinar beta, maka neutronnya berkurang dan protonnya bertambah.
Contoh:\[\\_0n^1 \rightarrow _1p^1 + _{(-1)}e^0 \\ _6C^{14} \rightarrow _7N^{14}+ _{(-1)}e^0\]
b) Melepaskan neutron
Contoh:\[\\_2He^5\rightarrow _2He^4+ _0n^1\]
2. Nuklida-nuklida di bawah pita kestabilan
Syarat: nuklida memiliki jumlah neutron (n) < proton (proton). Karena jumlah proton lebih banyak maka harus dikurangi dengan cara:
a) Melepaskan positron
Contoh:\[\\_1p^1 \rightarrow _0n^1 + _{(+1)}e^0 \\ _6C^{10} \rightarrow _5B^{10}+_{(+1)}e^0\]
b) Menangkap elektron
Dalam hal ini, elektron orbital, yaitu dari kulit K, diserap oleh inti. Elektron tersebut bergabung dengan proton membentuk neutron. Kekurangan elektron pada kulit K kemudian diisi oleh elektron dari kulit luar, disertai pemancaran enetrgi berupa sinar X.
Contoh:\[\\_1p^1 + _{(-1)}e^0 \rightarrow _0n^1 + _0\gamma ^0\\ _{37}Rb^{81} + _{(-1)}e^0 \rightarrow 36Kr81 + _0\gamma ^0\\ _4Be^7 + _{(-1)}e^0 \rightarrow _3Li^7 + _0\gamma ^0\\\]
3. Nuklida-nuklida di tepi atas kanan pita kestabilan (Z > 83)
Nuklida-nuklida ini menstabilkan unsurnya sendiri dengan memancarkan sinar alfa atau inti helium.
Contoh:\[\\_{92}U^{235} \rightarrow _{90}Th^{231} + _2He^4\]
C. Bilangan Ajaib
Dalam kestabilan inti, terdapat suatu istilah “Bilangan Ajaib”. Bilangan ajaib adalah nuklida dengan jumlah proton atau neutron sebanyak 2,8,20,28,50, dan 82 (juga 126 khusus untuk neutron). Jadi, unsur-unsur bilangan ajaib pasti selalu stabil alias tidak radioaktif.Contoh:
- 1. 2He4 = proton 2 dan neutron 2 = termasuk bilangan ajaib
2. 8O16 = proton 8 dan neutron 8 = termasuk bilangan ajaib
3. 20Ca40 = proton 20 dan neutron 20 = termasuk bilangan ajaib
4. 82Pb208 = proton 82 dan neutron = 126 = termasuk bilangan ajaib karena 126 harus milik neutron satu-satunya
D. Laju peluruhan
Laju peluruhan adalah seberapa cepat suatu zat radoiaktif meluruh. Laju peluruhan menandakan keaktifan zat radioaktif, dengan berbanding lurus terhadap konstanta dan jumlah nuklida radioaktif. Rumusnya: \[R=\lambda .N=n\lambda .N_{A}\]E. Waktu paruh
Waktu paro atau paruh adalah waktu yang diperlukan unsur radioaktif sehingga separo zat radoiaktif tersebut meluruh dari massa awalnya. Waktu paruh dilambang dengan T1/2. Rumusnya yaitu: \[T_{\frac{1}{2}}=\frac{ln2}{\lambda }=\frac{0,693}{\lambda }\]F. Umur rata-rata
Umur rata-rata adalah kebalikan dari peluang (hipotesis) untuk meluruh persatuan waktu. Dengan rumus: \[T_{max}=1,44.T_{\frac{1}{2}}\]G. Peluruhan inti
Dalam peluruhan inti inilah perhitungan radioaktif yang paling penting karena menyebabkan perbedaan jumlah partikel sebelum dan sesudah reaksi peluruhan. Berikut rumus peluruhan inti:\[\\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{n}\\\\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\N_{t}=N_{o}e^{-\lambda t}\]H. SOAL DAN PENYELESAIAN KESTABILAN INTI dan PELURUHAN RADIOAKTIF
1. Sejumlah 25 gram zat radioaktif disimpan selama 60 tahun. Jika waktu paruh zat tersebut adalah 20 tahun, massa zat radioaktif yang tersisa adalah…gramA. 3,125
B. 3,25
C. 3,75
D. 4,15
E. 6,25
Jawaban Fisika dari Pak Dimpun: B
\[\\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\N_{t}=25\left ( \frac{1}{2} \right )^{\frac{60}{20}}\\\\N_{t}=3,25gr\]
2. Setelah 10 tahun keaktifan unsur Telurium meluruh menjadi 300 dps, dengan keaktifan awal 2400 dps. Waktu paro zat radioaktif tersebut adalah…
A. 3 tahun
B. 6,5 tahun
C. 3,3 tahun
D. 1 tahun
E. 3,125 bulan
Jawaban Fisika dari Pak Dimpun: B
\[\\A_{t}=A_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\300=2400\left ( \frac{1}{2} \right )^{\frac{10}{T_{\frac{1}{2}}}} \\\\ \left ( \frac{1}{2} \right )^{3}=\left ( \frac{1}{2} \right )^{\frac{10}{T_{\frac{1}{2}}}} \\\\T_\frac{1}{2}=\frac{10}{3}\approx 3,3thn\]
3. Sebuah benda purbakala yang baru ditemukan memiliki massa 8 gram. Jika umur benda tersebut diperkirakan 2,610 tahun dengan waktu paruh 870 tahun, massa awal benda adalah…gram
A. 40
B. 48
C. 56
D. 64
E. 66
Jawaban Fisika dari Pak Dimpun: D
\[ \\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\8=N_{o}\left ( \frac{1}{2} \right )^{\frac{2610}{870}} \\\\ 8=N_{o}\left ( \frac{1}{2} \right )^{3} \\\\N_{o}=8x8=64gr\]
4. Suatu radioaktif mempunyai waktu paruh 18 hari. Jika unsur radioaktif tersebut disimpan selama 72 hari, sisa unsur radioaktif tersebut adalah…%
A. 3,12
B. 6,25
C. 12,5
D. 25
E. 50
Jawaban Fisika dari Pak Dimpun: B
\[ \\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\\frac{N}{N_{o}}=\left ( \frac{1}{2} \right )^{\frac{72}{18}} \\\\\frac{N}{N_{o}}=\left ( \frac{1}{2} \right )^{4} \\\\\frac{N}{N_{o}}=0,0625=6,25\%\]
5. Waktu paruh Bi-210 adalah 5 hari. Awalnya disimpan sebanyak 16 gram dan kemudian sisanya tinggal 1 gram, unsur tersebut telah disimpan selama....hari
A. 10
B. 15
C. 20
D. 25
E. 30
Jawaban Fisika dari Pak Dimpun: C
\[\\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\1=16\left ( \frac{1}{2} \right )^{\frac{t}{5}}\\\\\left ( \frac{1}{2} \right )^{4}=\left ( \frac{1}{2} \right )^{\frac{t}{5}}\\\\t=20\]
6. Untuk jumlah mol yang sama, maka zat radioaktif yang paling aktif ialah yang mempunyai waktu paro …
A. 4,5 milyar tahun
B. 65 tahun
C. 12 hari
D. 1 menit
E. 1 detik
Jawaban Fisika dari Pak Dimpun: E
Semakin singkat waktu paruh, semakin cepat zat radioaktif meluruh dan paling aktif
7. Sebuah fosil berupa tulang binatang ditemukan dalam tanah. Setelah diteliti dalam laboraturium teryata tulang tersebut mengandung sisa 25% C-14. Jika waktu parut dari C-14 adalah 5.730 tahun, maka umur fosil itu adalah …
A. 2865 tahun
B. 4297,5 tahun
C. 5730 tahun
D. 8595 tahun
E. 11.460 tahun
Jawaban Fisika dari Pak Dimpun: E
\[ \\N_{t}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\\frac{1}{4}N_{o}=N_{o}\left ( \frac{1}{2} \right )^{\frac{t}{5}}\\\\\left ( \frac{1}{2} \right )^{2}=\left ( \frac{1}{2} \right )^{\frac{t}{5730}}\\\\t=11.460\]
8. Suatu sampel isotop radioaktif (T1/2 = 6 hari) dibuat dan mulai disimpan pada tanggal 1 Juni 2005 dengan aktivitas spesifik 9600 cpm. Pada tanggal berapa aktivitasnya tinggal 300 cpm?
A. 7 Juni
B. 13 Juni
C. 19 Juni
D. 25 Juni
E. 1 Juli
Jawaban Fisika dari Pak Dimpun: E
\[ \\A_{t}=A_{o}\left ( \frac{1}{2} \right )^{\frac{t}{T_{\frac{1}{2}}}}\\\\300=9600\left ( \frac{1}{2} \right )^{\frac{t}{6}} \\\\ \left ( \frac{1}{2} \right )^{5}=\left ( \frac{1}{2} \right )^{\frac{t}{6}} \\\\t=30hari\] awal 1 Juni, 30 hari berarti 1 Juli.