Soal dan Penyelesaian Fisika - Latihan Soal dan Penyelesaian UTBK SBMPTN sebagai bahan Latihan dalam persiapan menghadapi Tes Kemampuan Akademik Saintek khususnya mata ujian Fisika pada Ujian Tulis Berbasis Komputer (UTBK) yaitu tes masuk ke perguruan tinggi yang dilaksanakan oleh Lembaga Tes Masuk Perguruan Tinggi (LTMPT).
1. Dua balok bermassa m = 1,0 kg dan M=2,0 kg saling terhubung dengan seutas tali seperti gambar dan bergerak tanpa slip melalui sebuah katrol dengan momen inersia 0,01 $kgm^{2}$ berputar dengan percepatan linear 2,5 $m/s^{2}$ dan percepatan gravitasi 10 $m/s^{2}$, jari - jari katrol adalah . . cm
A. 9,0
B. 10,0
C. 11,0
D. 12,0
E. 13,0
Penyelesaian Fisika:
\begin{align*} a=&\frac{\left(M-m\right)g}{M+m+\frac{I}{R^{2}}} \\2,5=&\frac{\left(2-1\right)10}{1+2+\frac{0,01}{R^{2}}} \\2,5=&\frac{10}{3+\frac{0,01}{R^{2}}} \\7,5+&\frac{0,025}{R^{2}}=10 \\\frac{0,025}{R^{2}}=&2,5 \\R^{2}=&\frac{0,025}{2,5} \\R^{2}=&0,01 \\R=&0,1\,\,m=10\,\,cm \end{align*}
2. Gerak lurus sebuah benda diperlihatkan pada gambar di bawah ini.
Kecepatan rata – rata benda tersebut antara t = 0 s dan t = 8 s adalah . . . . m/s
A. 4,50
B. 4,75
C. 5,00
D. 6,50
E. 7,00
Penyelesaian Fisika:
Perhatikan grafik
maka:
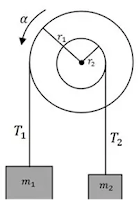
\begin{align*} v&=\frac{\textrm{perpindahan}}{\textrm{waktu}}\\&=\frac{\textrm{luas grafik}}{\textrm{waktu}} \\v&=\frac{L_{1}+L_{2}}{t}\\&=\frac{24+32}{8}=7\,\,ms^{-1}\end{align*} 3. Suatu sistem mekanik tersusun dari dua katrol berbentuk silinder yang ditempel sesumbu seperti pada gambar. Jari - jari $R_{1}= 10 cm$ dan $R_{2}= 5 cm$. Pada setiap katrol dililitkan seutas tali dengan beban diujungnya. Jika tegangan tali pada $m_{1} = 12,5 N$ dan $m_{2} = 15 N$ sedangkan percepatan linear beban $m_{2} = 2,5 m/s^{2} $ dan momen inersia katrol kedua adalah...
A. 0,01
B. 0,02
C. 0,03
D. 0,04
E. 0,05
Penyelesaian Fisika:
\begin{align*}R_{1}=& 10 cm ;\: R_{2}= 5 cm\\T_{1}=& 12,5 N;\: T_{2}=15 N\\a_{2}=&\alpha R_{2} \\2,5=&\alpha(0,05) \\\alpha=&50\,rad/s^{2}\end{align*}Katrol\begin{align*} \Sigma\tau=&I\alpha \\T_{1}R_{1}&-T_{2}R_{2}=I\alpha \\12,5(0,1)&-15(0,05)=I(50) \\0,5=&I(50) \\I=&0,01\,rad/s^{2} \end{align*}
4. Sebuah balok bermassa 5 kg bergerak pada sebuah bidang datar licin dengan kecepatan 2 m/s. Kemudian balok tersebut menuruni bidang miring kasar dengan kemiringan $37^o$ dan mengalami gaya gesek sebesar 20 N. Setelah sampai dasar bidang miring, balok meluncur pada bidang datar licin pada kecepatan 4 m/s. Jika percepatan gravitasi pada tempat tersebut 10 $m/s^{2}$, kedua bidang datar tersebut mempunyai perbedaan tinggi sebesar . . . .m
A. 0,8
B. 1,2
C. 1,5
D. 1,8
E. 2,0
Penyelesaian Fisika:
$Em_{awal}=Em_{akhir}\\Ep+Ek_{o}=W_{gesek}+Ek_{t}\\mgh+\frac{1}{2}mv_{o}^{2}=f_{gesek}.s+\frac{1}{2}mv_{t}^{2}\\mgh+\frac{1}{2}mv_{o}^{2}=f_{gesek}.\frac{h}{sin\,\,\theta}+\frac{1}{2}mv_{t}^{2} \\5.10.h+\frac{1}{2}.5.2^{2}=20.\frac{h}{0,6}+\frac{1}{2}.5.4^{2}\\50h+10=\frac{100h}{3}+40 \\\frac{50}{3}h=30 \\h=\frac{9}{5}m=1,8\,m$5. Dua buah balok bermassa $m_1$ = 1,0 kg dan $m_2$ = 2 kg dihubungkan dengan seutas tali yang bergerak tanpa slip melalui sebuah katrol (silinder pejal).
Massa katrol 2,0 kg dan berotasi bebas tanpa gesekan, radiusnya 10 cm, sedangkan permukaan kasar licin. Diketahui besar percepatan gravitasi setempat 10 $m/s^2$ , besar tegangan tali pada $m_1$ sama dengan ….N
A. 3,5
B. 4,0
C. 5,0
D. 7,5
E. 10,0
Penyelesaian Fisika:
\begin{align*} a=&\frac{m_{2}g}{m_{1}+m_{2}+\frac{1}{2}m_{k}}\\a=&\frac{2(10)}{1+2+\frac{1}{2}(2)}\\=&5\,ms^{-2} \end{align*} Tegangan tali benda 1 \begin{align*}T_{1}=m_{1}a=(1)(5)=5\,\,N \end{align*}
6. Sebuah balok bermassa 1 kg bergerak di bidang datar kasar kemudian mendaki sebuah bidang miring yang licin. Panjang bidang miring 1,0 m dan kemiringan $30^o$ . Mula – mula balok bergerak pada bidang datar kasar, gaya gesek balok dan bidang datar kasar sebesar 1,0 N. Usaha oleh gaya total yang bekerja pada balok sampai ujung lintasan bidang miring adalah -6 Joule. Jika percepatan gravitasi 10 $m/s^{2}$, panjang lintasan balok di bidang kasar adalah . . . . m
A. 5
B. 4
C. 3
D. 2
E. 1
Penyelesaian Fisika:
\begin{align*} W&=\Delta E_{k} \\W&=E_{k_2}-E_{k_1}\\-6&=0-E_{k_1} \\E_{k_1}&=6\,Joule\end{align*} Hukum kekekalan energi
\begin{align*} W&=\Delta E_{k} \\W&=E_{k_2}-E_{k_1}\\-6&=0-E_{k_1} \\E_{k_1}&=6\,Joule\end{align*} Hukum kekekalan energi
\begin{align*} E_{awal}&=E_{akhir} \\E_{k}&=W_{gsk}+E_{p} \\E_{k}&=f_{gsk}S+mgS\,sin\theta \\6&=1.S+1.10.1.\,\sin 30^{o} \\6&=S+1.10.1.\,(0,5) \\6&=S+5 \\S&=1\,m \end{align*}
7. Sebuah partikel bermuatan q dan bermassa m masuk dalam suatu daerah bermedan magnet homogen B. Jika lintasan partikel dalam medan magnet berbentuk lingkaran dengan kecepatan v, maka jari – jari partikel tersebut adalah?
A. $\frac{mB}{qv} $
B. $\frac{mq}{vB} $
C. $\frac{m}{q}\left(\frac{v}{B}\right)^{2} $
D. $\frac{mv}{qB} $
E. $\frac{mv^{2}}{qB} $
Penyelesaian Fisika:
Gaya Lorentz pada muatan bergerak masuk dalam daerah medan magnet membentuk lintasan melingkar berlaku:\begin{align*} F_{L}=&F_{sp} \\Bqv=&\frac{mv^{2}}{R} \\R=&\frac{mv}{Bq} \end{align*} 8. Muatan titik A 1 µC berada di x =0 cm dan muatan titik 4 µC berada di x = 60 cm. Di titik x = 30 cm diletakkan muatan titik C. Jika energi potensial sistem sama dengan nol, muatan titik C sama dengan . . . . µC
A. -0,2
B. +0,2
C. -0,4
D. +0,4
D. -0,
Penyelesaian Fisika:
Perhatikan skema soal:
\begin{align*}E_{p_tot}=E_{p_{AB}}+E_{p_{AC}}+E_{p_{BC}}\end{align*} 9. Dua buah muatan A dan B masing – masing 2 µC dan 32 µC berjarak 60 cm satu sama lain. Sebuah titik C berada di antara kedua muatan mengalami medan listrik sama dengan nol. Perbandingan jarak muatan A dan B terhadap titik C adalah?
A. 4 : 1
B. 1 : 4
C. 2 : 3
D. 1 : 5
E. 3 : 2
Penyelesaian Fisika:
Karena kedua muatan listrik sejenis, maka daerah yang bernilai medan listriknya nol adalah diantara kedua muatan dan dekat muatan 1 karena lebih kecil.
Maka:$\frac{Q_{1}}{r_{1}^{2}}=\frac{Q_{2}}{r_{2}^{2}}\\\frac{r_{1}^{2}}{r_{2}^{2}}=\frac{Q_{1}}{Q_{2}} \\\frac{r_{1}}{r_{2}}=\sqrt{\frac{Q_{1}}{Q_{2}}} \\\frac{r_{1}}{r_{2}}=\sqrt{\frac{2}{32}} \\\frac{r_{1}}{r_{2}}=\frac{1}{4}$
10. Dua sumber bunyi A dan B serta pengamat O terletak di sumbu x, sebagaimana pada gambar.
A. 0,1
B. 0,2
C. 0,3
D. 0,4
E. 0,5
Penyelesaian Fisika:
Frekuensi Pelayangan
\begin{align*} f_{\textrm{pelayangan}}=&f_{pA}-f_{pB} \\\frac{2}{15}f=\left (\frac{v}{v-0,25v} \right )&f-\left (\frac{v}{v-bv} \right )f \\\frac{2}{15}=\frac{v}{0,75v}&-\frac{v}{(1-b)v} \\\frac{2}{15}=&\frac{4}{3}-\frac{1}{(1-b)} \\\frac{1}{1-b}=&\frac{4}{3}-\frac{2}{15} \\\frac{1}{1-b}=&\frac{20-2}{15} \\\frac{1}{1-b}=&\frac{18}{15} \\\frac{1}{1-b}=&\frac{6}{5} \\5=&6-6b \\6b=&1 \\b=&\frac{1}{6} \end{align*}
Penyelesaian Fisika:
Frekuensi Pelayangan
\begin{align*} f_{\textrm{pelayangan}}=&f_{pA}-f_{pB} \\\frac{2}{15}f=\left (\frac{v}{v-0,25v} \right )&f-\left (\frac{v}{v-bv} \right )f \\\frac{2}{15}=\frac{v}{0,75v}&-\frac{v}{(1-b)v} \\\frac{2}{15}=&\frac{4}{3}-\frac{1}{(1-b)} \\\frac{1}{1-b}=&\frac{4}{3}-\frac{2}{15} \\\frac{1}{1-b}=&\frac{20-2}{15} \\\frac{1}{1-b}=&\frac{18}{15} \\\frac{1}{1-b}=&\frac{6}{5} \\5=&6-6b \\6b=&1 \\b=&\frac{1}{6} \end{align*}
D. FISIKA MODEREN
11. Sebuah partikel bermassa diam mo bergerak dengan kecepatan v. Jika energi kinetic partikel tersebut $E_{k}=\frac{2}{3}m_{o}c^2$ maka v =
11. Sebuah partikel bermassa diam mo bergerak dengan kecepatan v. Jika energi kinetic partikel tersebut $E_{k}=\frac{2}{3}m_{o}c^2$ maka v =
A. 0,25 c
B. 0,50 c
C. 0,60 c
D. 0,75 c
E. 0,80 c
Penyelesaian Fisika:
Relativitas Khusus \begin{align*} E_{k}=&E_o\left(\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}-1\right) \\\frac{2}{3}m_{o}c^{2}=&m_{o}c^{2}\left(\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}-1\right) \\\frac{2}{3}=&\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}-1 \\\frac{5}{3}=&\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \\\frac{25}{9}=&\frac{1}{1-\frac{v^{2}}{c^{2}}} \\25-25\frac{v^2}{c^2}&=9\\\frac{v^{2}}{c^{2}}=&\frac{16}{25} \\v^{2}=&\frac{16}{25}c^{2} \\v=&\frac{4}{5}c =0,8c \end{align*} 12. Pada percobaan efek fotolistrik, diperoleh potensial penghenti $V_{1}$ untuk penyinaran dengan panjang gelombang 500 nm dan potensial penghenti 2,0 V untuk penyinaran dengan panjang gelombang 400 nm. Jika panjang gelombang ambang untuk logam target sama dengan 600 nm, nilai $V_{1}$ sama dengan . . . .
A. 1,0 V
B. 0,9 V
C. 0,8 V
D. 0,7 V
E. 0,6 V
Penyelesaian Fisika:
\begin{align*} Ek=&E-E_{o} \\qV=&hc\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right) \\V=&\frac{hc}{q}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right) \\\frac{V_{1}}{V_{2}}=&\frac{\left(\frac{1}{\lambda_{1}}-\frac{1}{\lambda_{o}}\right)}{\left(\frac{1}{\lambda_{2}}-\frac{1}{\lambda_{o}}\right)} \\\frac{V_{1}}{V_{2}}=&\frac{\frac{\lambda_{o}-\lambda_{1}}{\lambda_{1}\lambda_{o}}}{\frac{\lambda_{o}-\lambda_{2}}{\lambda_{2}\lambda_{o}}} \\\frac{V_{1}}{V_{2}}=&\frac{\left(\lambda_{o}-\lambda_{1}\right)\lambda_{2}}{\left(\lambda_{o}-\lambda_{2}\right)\lambda_{1}} \\\frac{V_{1}}{2}=&\frac{\left(600-500\right)400}{\left(600-400\right)500} \\\frac{V_{1}}{2}=&\frac{4}{10} \\V_{1}=&\frac{4}{5}=0,8\,volt\end{align*} 13. Pada suatu percobaan efek fotolistrik diperoleh nilai $\small {\frac{hc}{e}=12,4\times10^{-7}\,Jm/C}$ dengan h tetapan Planck, c kelajuan cahaya dalam vakum dan e muatan elektron. Energi kinetik maksimum yang mungkin dimiliki elektron yang lepas sama dengan 1,03 eV ketika percobaan dilakukan dengan foton berpanjang gelombang 400 nm. Panjang gelombang ambang untuk logam target sama dengan . . . . nm.
A. 450
B. 500
C. 550
D. 600
E. 650
Penyelesaian Fisika:
Efek Fotolistrik
\[\small {E_{k}=1,03\,eV\\E_{k}=1,03\times1,6\times10^{-19}\,J \\V=\frac{E_{k}}{q}=\frac{1,03\times1,6\times10^{-19}}{1,6\times10^{-19}}\\V=1,03\,Volt}\]Energi Kinetik\[\small {Ek=E-E_{o}\\ qV=hc\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right) \\V=\frac{hc}{q}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right) \\1,03=12,4\times10^{-7}\left(\frac{1}{400\times10^{-9}}-\frac{1}{\lambda_{o}}\right) \\\frac{1,03}{12,4\times10^{-7}}=\frac{1}{4\times10^{-7}}-\frac{1}{\lambda_{o}} \\0,083\times10^{7}=0,25\times10^{7}-\frac{1}{\lambda_{o}} \\0,167\times10^{7}=\frac{1}{\lambda_{o}} \\\lambda_{o}=\frac{1}{0,167\times10^{7}} \\\lambda_{o}=5,988\times10^{-7}m \\\lambda_{o}=600\,nm}\]
Efek Fotolistrik
\[\small {E_{k}=1,03\,eV\\E_{k}=1,03\times1,6\times10^{-19}\,J \\V=\frac{E_{k}}{q}=\frac{1,03\times1,6\times10^{-19}}{1,6\times10^{-19}}\\V=1,03\,Volt}\]Energi Kinetik\[\small {Ek=E-E_{o}\\ qV=hc\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right) \\V=\frac{hc}{q}\left(\frac{1}{\lambda}-\frac{1}{\lambda_{o}}\right) \\1,03=12,4\times10^{-7}\left(\frac{1}{400\times10^{-9}}-\frac{1}{\lambda_{o}}\right) \\\frac{1,03}{12,4\times10^{-7}}=\frac{1}{4\times10^{-7}}-\frac{1}{\lambda_{o}} \\0,083\times10^{7}=0,25\times10^{7}-\frac{1}{\lambda_{o}} \\0,167\times10^{7}=\frac{1}{\lambda_{o}} \\\lambda_{o}=\frac{1}{0,167\times10^{7}} \\\lambda_{o}=5,988\times10^{-7}m \\\lambda_{o}=600\,nm}\]
14. Di suatu tempat vakum udara benda yang berukuran sangat kecil dengan massa diam sebesar mo ditembakkan sehingga bergerak dengan kecepatan 0,8 c. Energi total dan energi kinetik benda tersebut sebesar?
A. 5/3 $m_{o}c^{2} $ dan 2/3 $m_{o}c^{2} $
B. 2/3 $m_{o}c^{2}$ dan 5/3 $m_{o}c^{2} $
C. 3/5 $m_{o}c^{2}$ dan 4/5 $m_{o}c^{2} $
D. 4/5 $m_{o}c^{2}$ dan 3/5 $m_{o}c^{2} $
E. 1/3 $m_{o}c^{2}$ dan 2/3 $m_{o}c^{2} $
B. 2/3 $m_{o}c^{2}$ dan 5/3 $m_{o}c^{2} $
C. 3/5 $m_{o}c^{2}$ dan 4/5 $m_{o}c^{2} $
D. 4/5 $m_{o}c^{2}$ dan 3/5 $m_{o}c^{2} $
E. 1/3 $m_{o}c^{2}$ dan 2/3 $m_{o}c^{2} $
Penyelesaian Fisika:
Energi Total Relativitas
\begin{align*}E=&\frac{E_{o}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \\E=&\frac{m_{o}c^{2}}{\sqrt{1-\frac{\left(0,8c\right)^{2}}{c^{2}}}} \\E=&\frac{m_{o}c^{2}}{\sqrt{1-\frac{0,64c^{2}}{c^{2}}}} \\E=&\frac{m_{o}c^{2}}{\sqrt{0,36}} \\E=&\frac{m_{o}c^{2}}{0,6} \\E=&\frac{5}{3}m_{o}c^{2} \end{align*}
Energi Total Relativitas
\begin{align*}E=&\frac{E_{o}}{\sqrt{1-\frac{v^{2}}{c^{2}}}} \\E=&\frac{m_{o}c^{2}}{\sqrt{1-\frac{\left(0,8c\right)^{2}}{c^{2}}}} \\E=&\frac{m_{o}c^{2}}{\sqrt{1-\frac{0,64c^{2}}{c^{2}}}} \\E=&\frac{m_{o}c^{2}}{\sqrt{0,36}} \\E=&\frac{m_{o}c^{2}}{0,6} \\E=&\frac{5}{3}m_{o}c^{2} \end{align*}
Energi Kinetik Relativitas
\begin{align*}E_{k}=&E-E_{o} \\E_{k}=&\frac{5}{3}E_{o}-E_{o} \\E_{k}=&\frac{2}{3}E_{o} \\E_{k}=&\frac{2}{3}m_{o}c^{2} \end{align*}
\begin{align*}E_{k}=&E-E_{o} \\E_{k}=&\frac{5}{3}E_{o}-E_{o} \\E_{k}=&\frac{2}{3}E_{o} \\E_{k}=&\frac{2}{3}m_{o}c^{2} \end{align*}
15. Gas ideal monotomik sebanyak n mol menjalani proses termodinamika dalam wadah yang volumenya tetap b $m^{3}$. Dalam proses tersebut gas mengalami perubahan tekanan sebesar a Pa. Perubahan energi dalam gas sebesar .... J.
A. 3ab/2B. 2ab
C. 5ab/2
D. 3ab
E. 7ab/2
Penyelesaian Fisika:
Perubahan energi dalam
\begin{align*}\Delta U=&\frac{3}{2}nR\Delta T \\\Delta U=&\frac{3}{2}nR(T_{2}-T_{1}) \\\Delta U=&\frac{3}{2}(nRT_{2}-nRT_{1}) \\\Delta U=&\frac{3}{2}(P_{2}V-P_{1}V) \\\Delta U=&\frac{3}{2}(P_{2}-P_{1})V \\\Delta U=&\frac{3}{2}\Delta P\,V \\\Delta U=&\frac{3}{2}ab \end{align*}
Penyelesaian Fisika:
Perubahan energi dalam
\begin{align*}\Delta U=&\frac{3}{2}nR\Delta T \\\Delta U=&\frac{3}{2}nR(T_{2}-T_{1}) \\\Delta U=&\frac{3}{2}(nRT_{2}-nRT_{1}) \\\Delta U=&\frac{3}{2}(P_{2}V-P_{1}V) \\\Delta U=&\frac{3}{2}(P_{2}-P_{1})V \\\Delta U=&\frac{3}{2}\Delta P\,V \\\Delta U=&\frac{3}{2}ab \end{align*}
