SOAL DAN PENYELESAIAN RANGKAIAN LISTRIK ARUS SEARAH (DC)

Cara Pintar Cepat Pintar Fisika - Contoh Soal dan Penyelesaian Rangkaian Listrik Arus Searah.

Berikut adalah Materi Fisika kelas 12 SMA. Khusus membahas tentang rangkaian listrik arus searah konsep rangkaian  tertutup satu loop, dua loop, rangkaian seri, rangkaian paralel dan rangkaian  campuran, termasuk daya dan energi listrik.

SOAL DAN PENYELESAIAN RANGKAIAN LISTRIK ARUS SEARAH (DC)

---

1. Tiga buah hambatan masing-masing 2 Ω, 3Ω, dan 4Ω disusun secara seri, lalu dihubungkan dengan beda potensial 9 volt. Tentukan :
a. Besar hambatan pengganti atau hambatan total;
b. Besar arus pada rangkaian;
c. Beda potensial pada ujung-ujung masing-masing hambatan.

Jawaban Fisika dari Pak Dimpun:
a. Hambatan total $$\small \\{{R}_{tot}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$$ $$\small \\{{R}_{tot}}=2+3+4\\\\ {{R}_{tot}}=9\text{ }\Omega$$ b. Arus pada rangkaian $$\small \\I=\frac{V_{tot}}{R_{tot}}\\\\I=\frac{9}{9}\\\\I=1\text{ A}$$
c. Beda potensial pada ujung-ujung masing-masing hambatan. $$\small \\ V_{1}=I.R_{1}=1x2=2volt \\\\V_{2}=I.R_{2}=1x3=3volt \\\\V_{3}=I.R_{3}=1x4=4volt$$

---

2. Tiga buah hambatan masing-masing 2 Ω, 3Ω, dan 6Ω disusun secara paralel, lalu dihubungkan dengan beda potensial 3 volt. Tentukan :
a. Besar hambatan pengganti atau hambatan total;
b. Besar arus pada rangkaian;
c. Beda potensial pada ujung-ujung masing-masing hambatan.
Jawaban Fisika dari Pak Dimpun:
a. Hambatan pengganti $$\frac{1}{R_{tot}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}\\\\\frac{1}{R_{tot}}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\\\\ \frac{1}{R_{tot}}=\frac{6+4+2}{12}\\\\R_{tot}=1\Omega$$ b. Besar arus pada rangkaian;
$$\small \\ i=\frac{V}{{{R}_{total}}}\\\\i=\frac{3}{1}=3\text{ A}$$ c. Besar arus yang mengalir pada masing-masing hambatan $$\small \\{{i}_{1}}=\frac{{{V}_{1}}}{{{R}_{1}}}=\frac{3}{2}=1,5\text{ A}\\\\ {{i}_{2}}=\frac{{{V}_{2}}}{{{R}_{2}}}=\frac{3}{3}=1\text{ A}\\\\{{i}_{3}}=\frac{V}{{{R}_{3}}}=\frac{3}{6}=0,5\text{ A}$$

---

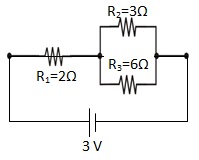
3. Perhatikan tiga buah hambatan listrik di susun seperti gambar di bawah ini !

Hambatan pertama memiliki besar hambatan 2 Ω, hambatan kedua 3 Ω, hambatan ketiga 6 Ω. Ketiga hambatan tersebut dihubungkan ke sumber tegangan listrik 3 volt. Tentukan :
a.Besar hambatan pengganti;
b.Besar arus total;
c.Beda potensial pada masing-masing ujung hambatan;
d.Besar arus yang melewati hambatan 3Ω dan hambatan 6Ω !
Jawaban Fisika dari Pak Dimpun:
a. Menentukan besar hambatan pengganti
PERTAMA kita gabungkan hambatan 3 Ω dan 6 Ω (paralel): $$\small \\\frac{1}{{{R}_{23}}}=\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}$$ $$\small \\\frac{1}{{{R}_{23}}}=\frac{1}{3}+\frac{1}{6}$$ $$\small \\\frac{1}{{{R}_{23}}}=\frac{2+1}{6}\\\\R_{23}=2\text{ }\Omega$$ Sekarang gambar soal menjadi:

Hambatan total: $$\small \\{{R}_{tot}}={{R}_{1}}+{{R}_{23}}\\\\ {{R}_{tot}}=2+2=4\text{ }\Omega$$ b. Besar arus pada rangkaian $$\small \\I=\frac{V}{{{R}_{tot}}}=\frac{3}{4}=0,75\text{ A}$$ c.Beda potensial pada masing masing hambatan $$\small \\{{V}_{1}}=I{{R}_{1}}\\\\V=0,75\times 2=1,5\text{ volt}\\\\V_{23}=I.R_{23}\\\\V_{23}=0,75x 2\\\\V_{23}=1,5Volt\\\\V_{2}=V_{3}=V_{23}$$ d.Besar arus listrik yang melewati hambatan kedua adalah $$\small \\I_{2}=\frac{{{V}_{2}}}{{{R}_{2}}}\\\\I_{2}=\frac{{{V}_{23}}}{{{R}_{2}}}\\\\I_{2}=\frac{1,5}{3}=0,5\text{ A}$$ Besar arus listrik yang melewati hambatan ketiga adalah: $$\small \\I_{3}=\frac{{{V}_{3}}}{{{R}_{3}}}\\\\I_{3}=\frac{{{V}_{23}}}{{{R}_{3}}}\\\\I_{3}=\frac{1,5}{6}\\\\I_{3}=0,25\text{ A}$$

---

4. Perhatikan gambar di bawah ini !

Hambatan pertama memiliki besar hambatan 2 Ω, hambatan kedua 4 Ω, hambatan ketiga 3 Ω. Besar arus yang melewati hambatan 3Ω adalah 1 A. Tentukan :
a. Besar potensial sumber;
b. Besar arus yang melewati hambatan 1 dan hambatan 2 !
Jawaban Fisika dari Pak Dimpun:
a. Besar potensial sumber $$\small \\V={{I}_{3}}{{R}_{3}}=3\text{ volt}$$ b. Besar arus yang melewati hambatan pertama dan hambatan kedua $$\small \\I_{12}=\frac{{{V}_{12}}}{{{R}_{12}}}\\\\I_{12}=\frac{{{V}_{12}}}{{{R}_{1}}+{{R}_{2}}}\\\\I_{12}=\frac{3}{6}=0,5\text{ A}$$