Ini pertanyaannya:
Sebuah tangga AB homogen panjangnya 5 m dan beratnya 100 N. ujung A terletak pada lantai datar dan ujung B bersandar pada tembok vertikal. Ujung A berjarak 3 m dari tembok dan koefisien gesek statik ujung A dan B sama, yaitu 0,5. Jarak terjauh dari ujung A yang dapat dicapai orang yang beratnya 500 N jika orang tersebut memanjat tangga sebelum tangga tergelincir adalah...
a. 3,5m
b. 3,6m
c. 3,7m
d. 3,8m
e. 3,9m
Teman-teman juga mungkin pernah dihadapkan dengan soal ini, dan mencoba mencari jawaban melalui om google, mbak yahoo, paman bing dll.
Sayangnya, beberapa penyelesaian yang saya temukan memberikan hasil yang belum tepat, (termasuk pada website yang iklannya mungkin muncul di blog ini) karena semua penyelesaian yang saya temukan mengabaikan koefisien gesekan dinding, dan tentu saja menjadi salah.
Kali ini, Pak Dimpun akan mencoba menyelesaikan secara ringkas, dan semoga bermanfaat...

Sebuah tangga AB homogen panjangnya 5 m dan beratnya 100 N. ujung A terletak pada lantai datar dan ujung B bersandar pada tembok vertikal. Ujung A berjarak 3 m dari tembok dan koefisien gesek statik ujung A dan B sama, yaitu 0,5. Jarak terjauh dari ujung A yang dapat dicapai orang yang beratnya 500 N jika orang tersebut memanjat tangga sebelum tangga tergelincir adalah...
a. 3,5m
b. 3,6m
c. 3,7m
d. 3,8m
e. 3,9m
Teman-teman juga mungkin pernah dihadapkan dengan soal ini, dan mencoba mencari jawaban melalui om google, mbak yahoo, paman bing dll.
Sayangnya, beberapa penyelesaian yang saya temukan memberikan hasil yang belum tepat, (termasuk pada website yang iklannya mungkin muncul di blog ini) karena semua penyelesaian yang saya temukan mengabaikan koefisien gesekan dinding, dan tentu saja menjadi salah.
Kali ini, Pak Dimpun akan mencoba menyelesaikan secara ringkas, dan semoga bermanfaat...

Jumlah gaya sumbu x dan sumby y:\[\\\Sigma F_{x}=0\\f_{A}=N_{B}.........(1)\]\[\\\Sigma F_{y}=0\\f_{B}+N_{A}=W_{t}+W_{o}....(2)\]gaya gesekan di A: \[\\f_{A}=\mu N_{A}....(3)\]gantikan $f_A$ dari persamaan (1) maka \[\\N_{B}=\mu N_{A}....(4)\]gaya gesekan di B: \[\\f_{B}=\mu N_{B}\]gantikan $N_B$ dari persamaan (4) maka \[\\f_{B}=\mu.\mu.N_{A}\\f_{B}=\mu^{2}N_{A}......(5)\]gantikan $f_B$ di persamaan (2), menjadi:\[\\\mu ^{2}N_{A}+N_{A}=W_{t}+W_{o} \\ \\N_{A}(\mu ^{2}+1)=W_{t}+W_{o}\\ \\N_{A}((0,5)^{2}+1)=100+500\\\\ N_{A}=\frac{600}{1,25}=480N\]masukkan nilai NA ke persamaan (3):\[\\f_{A}=0,5x480=240N\]kita ke persamaan (5): \[\\f_{B}=\mu^{2} N_{A}\\f_{B}=(0,5)^{2}x 480\\f_{B}=120N\]Langkah terakhir, kita gunakan jumlah momen gaya di titik A = 0.\[\small \Sigma \tau _{A}=0 \\N_{B}\sin \beta (L)+f_{B}\cos \beta (L) =\\W_{o} \cos \beta (x)+W_{t}\cos \beta (\frac{1}{2}L) \\\\240.\frac{4}{4}.5+120.\frac{3}{5}.5=\\500.\frac{3}{5}x+100.\frac{3}{5}.\frac{1}{2}.5\\300x=1170\\x=3,9m\]
kunci E.
Kami tambahkan satu soal lagi ya...!
Seorang naik tangga homogen yang disandarkan pada dinding vertikal licin dengan sudut kemiringan tertentu seperti tampak pada gambar.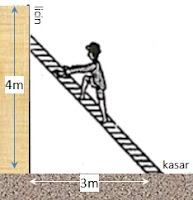
Kami tambahkan satu soal lagi ya...!
Seorang naik tangga homogen yang disandarkan pada dinding vertikal licin dengan sudut kemiringan tertentu seperti tampak pada gambar.

Berat tangga 300 N dan berat orang 700 N. Bila orang tersebut dapat naik sejauh 3 m sesaat sebelum tangga itu tergelincir, maka koefisien gesekan antara lantai dan tangga adalah...
A. 0,14
B. 0,43
C. 0,49
D. 0,50
E. 0,85
Penyelesaian Fisika dari Pak Dimpun: B
A. 0,14
B. 0,43
C. 0,49
D. 0,50
E. 0,85
Penyelesaian Fisika dari Pak Dimpun: B

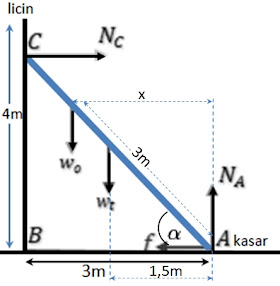
Panjang batang AC, misalkan L:
$\small \begin{align*}AC&=\sqrt{AB^2+BC^2}\\L&=\sqrt{3^2+4^2}=5m\end{align*}$
Panjang x:
$\begin{align*} \cos \alpha&=\frac{3}{5}=\frac{x}{3}\\x&=\frac{3\times3}{5}\\&=1,8m \end{align*}$
Jumlah momen gaya di A = 0.
$\begin{align*}\Sigma \tau _A &= 0\\N_C . 4 &= w_t.1,5+w_o.(x) \\N_C . 4 &= w_t.1,5 - w_o.1,8\\4N_C &= 300.1,5 - 700.1,8\\4N_C &= 450 + 1260\\4N_C &= 1710\\N_C &= 427,5\ N\end{align*}$
Jumlah gaya sumbu y = 0.
$\begin{align*}\Sigma F_y &= 0\\N_A &= w_o + w_t\\N_A &= 300 + 700\\N_A &= 1000N\end{align*}$
Jumlah gaya sumbu x = 0.
$\begin{align*}\Sigma F_x &= 0\\N_C &= f\\N_C &= \mu_s.N_A\\427,5 &= \mu_s.1000\\\mu_s &= \frac{427,5}{1000}\\\mu_s &= 0,4275\\\mu_s &= 0,43\end{align*}$
$\small \begin{align*}AC&=\sqrt{AB^2+BC^2}\\L&=\sqrt{3^2+4^2}=5m\end{align*}$
Panjang x:
$\begin{align*} \cos \alpha&=\frac{3}{5}=\frac{x}{3}\\x&=\frac{3\times3}{5}\\&=1,8m \end{align*}$
Jumlah momen gaya di A = 0.
$\begin{align*}\Sigma \tau _A &= 0\\N_C . 4 &= w_t.1,5+w_o.(x) \\N_C . 4 &= w_t.1,5 - w_o.1,8\\4N_C &= 300.1,5 - 700.1,8\\4N_C &= 450 + 1260\\4N_C &= 1710\\N_C &= 427,5\ N\end{align*}$
Jumlah gaya sumbu y = 0.
$\begin{align*}\Sigma F_y &= 0\\N_A &= w_o + w_t\\N_A &= 300 + 700\\N_A &= 1000N\end{align*}$
Jumlah gaya sumbu x = 0.
$\begin{align*}\Sigma F_x &= 0\\N_C &= f\\N_C &= \mu_s.N_A\\427,5 &= \mu_s.1000\\\mu_s &= \frac{427,5}{1000}\\\mu_s &= 0,4275\\\mu_s &= 0,43\end{align*}$







