Berikut kita bahas
SOAL DAN PENYELESAIAN DINAMIKA ROTASI KELAS 11
sebagai bahan belajar buat teman-teman.
1. Sebuah partikel bermassa 0,1 gram bergerak mengelilingi sumbu y dengan besar jari-jari 4 cm. Benda tersebut berputar dengan percepatan sudut 1 rad.s-2. Tentukanlah besar:
a. momen inersia;
b. momen gaya;
c. kecepatan sudut detik ke-2, benda mula-mula diam;
d. kecepatan linier pada detik ke-2, benda mula-mula diam; !
Jawaban Fisika Pak Dimpun
a. momen inersia partikel\begin{align*} I&=\Sigma m.R^2\\I&=0,1\times (4)^2\\I&=1,6\text{ gram.cm}^{2}\\I&=1,6\times 10^{-7}\text{ kg.m}^{2}\end{align*} b. momen gaya: \begin{align*} \tau &=I.\alpha \\\tau &=1,6\times 10^{-7}(1)\\\tau &=1,6\times 10^{-7}Nm\end{align*} c. kecepatan sudut saat detik kedua \begin{align*}\omega _{t}&=\omega _{o}+\alpha t\\\omega _{t}&=0+(1)(2)\\\omega _{t}&=2\text{ rad.s}^{-1}\end{align*} d. kecepatan linier detik ke-2\begin{align*}a&=\alpha .R\\a&=(1)4.10^{-2}\\a&=0,04ms^{-2}\\\\v&=\omega .R\\v&=(2)(0,04)\\v&=0,08ms^{-1}\end{align*}
2.Dua buah benda kecil bermassa 0,2gram dan 0,1gram berada pada bidang koordinat sumbu x dan sumbu y. Benda pertama berada pada koordinat (4,3), benda berada pada koordinat (-2,-2), sumbu x dan sumbu y bersatuan cm.
Tentukanlah besar momen inersia sistem dua benda jika:
a. berputar terhadap sumbu x;
b. berputar terhadap sumbu y;
Jawaban Fisika Pak Dimpun

a. Momen inersia terhadap sumbu x\begin{align*}I&=m_1r_1^{2}+m_2r_2^{2}\\I&=(0,2)(3)^{2}+(0,1)(2)^{2}\\I&=2,2\text{ gram.cm}^{2}\\I&=2,2.10^{-7}\text{ kg.m}^{2}\end{align*}
b. Momen inersia terhadap sumbu y\begin{align*}I&=m_1r_1^{2}+m_2r_2^{2}\\I&=(0,2)(4)^{2}+(0,1)(2)^{2}\\I&=3,6gram.cm^{2}\\I&=3,6.10^{-7}kg.m^{2}\end{align*}
3. Sebuah silinder pejal bermassa 400 gram berjari-jari 2 cm berada di titik A pada ketinggian 80 cm menggelinding tanpa slip pada bidang miring kasar AB tanpa kecepatan awal. Sudut kemiringan 37o.
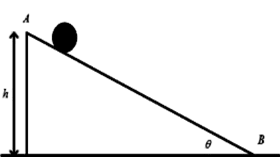
3. Sebuah silinder pejal bermassa 400 gram berjari-jari 2 cm berada di titik A pada ketinggian 80 cm menggelinding tanpa slip pada bidang miring kasar AB tanpa kecepatan awal. Sudut kemiringan 37o.

Tentukanlah besar:
a. percepatan silinder ketika sampai di dasar bidang miring (titik B);
b. kecepatan silinder ketika menuruni bidang miring;
c. gaya gesek ketika menuruni bidang miring;
d. koefisien gesek bidang miring dan silinder;
e. momen gaya ketika menuruni bidang miring; !
Jawaban Fisika Pak Dimpun
a. percepatan silinder ketika sampai di dasar bidang miring (titik B);
Perhatikan gambar;

Jika momen inersia kita tuliskan I=kmR2 maka:
Analisa gerak rotasi:\begin{align*}\tau &=I\alpha \\f.R&=kmR^2.\frac{a}{R}\\f&=kma....(1)\end{align*}Analisa gerak translasi:\begin{align*}&W\sin \theta -f=ma\\&f=mg\sin \theta -ma....(2)\end{align*}Substitusi kedua persamaan:\begin{align*}f&=mg\sin \theta -ma....(2)\\f&=kma....(1) \text{ -}\\\hline g&\sin \theta -a=ka\\a&=\frac{g\sin \theta }{k+1}\\a&=\frac{10(0,6)}{\frac{1}{2}+1}\\a&=4ms^{-2}\end{align*} kecepatan ketika menuruni bidang miring;\begin{align*}v_{B}^{2}&=v_{A}^{2}+2as\\v_{B}^{2}&=0+2a(\frac{h}{\sin \theta })\\v_{B}^{2}&=2(4)\frac{0,8}{0,6}\\v_{B}&=\frac{4}{3}\sqrt{6}\: m.s^{-1}\end{align*}c. gaya gesek ketika menuruni bidang miring;\begin{align*}f&=kma\\f&=\frac{1}{2}(0,4)(4)\\f&=0,8N\end{align*}d. koefisien gesek bidang miring dan silinder;\begin{align*}f&=\mu mg\cos \theta \\0,8&=\mu (0,4)(10)(0,8)\\\mu&=0,25N\end{align*} e. momen gaya ketika menuruni bidang miring;\begin{align*}\tau &=I\alpha \\\tau &=kmR^2.\frac{a}{R}\\\tau &=kmaR\\\tau &=\frac{1}{2}(0,4)(4)(0,02)\\\tau &=0,016Nm\end{align*}
4. Dua buah benda diikat dengan tali yang dianggap tak bermassa kemudian talinya disangkutkan pada sebuah katrol seperti pada gambar.

a. percepatan silinder ketika sampai di dasar bidang miring (titik B);
b. kecepatan silinder ketika menuruni bidang miring;
c. gaya gesek ketika menuruni bidang miring;
d. koefisien gesek bidang miring dan silinder;
e. momen gaya ketika menuruni bidang miring; !
Jawaban Fisika Pak Dimpun
a. percepatan silinder ketika sampai di dasar bidang miring (titik B);
Perhatikan gambar;

Jika momen inersia kita tuliskan I=kmR2 maka:
Analisa gerak rotasi:\begin{align*}\tau &=I\alpha \\f.R&=kmR^2.\frac{a}{R}\\f&=kma....(1)\end{align*}Analisa gerak translasi:\begin{align*}&W\sin \theta -f=ma\\&f=mg\sin \theta -ma....(2)\end{align*}Substitusi kedua persamaan:\begin{align*}f&=mg\sin \theta -ma....(2)\\f&=kma....(1) \text{ -}\\\hline g&\sin \theta -a=ka\\a&=\frac{g\sin \theta }{k+1}\\a&=\frac{10(0,6)}{\frac{1}{2}+1}\\a&=4ms^{-2}\end{align*} kecepatan ketika menuruni bidang miring;\begin{align*}v_{B}^{2}&=v_{A}^{2}+2as\\v_{B}^{2}&=0+2a(\frac{h}{\sin \theta })\\v_{B}^{2}&=2(4)\frac{0,8}{0,6}\\v_{B}&=\frac{4}{3}\sqrt{6}\: m.s^{-1}\end{align*}c. gaya gesek ketika menuruni bidang miring;\begin{align*}f&=kma\\f&=\frac{1}{2}(0,4)(4)\\f&=0,8N\end{align*}d. koefisien gesek bidang miring dan silinder;\begin{align*}f&=\mu mg\cos \theta \\0,8&=\mu (0,4)(10)(0,8)\\\mu&=0,25N\end{align*} e. momen gaya ketika menuruni bidang miring;\begin{align*}\tau &=I\alpha \\\tau &=kmR^2.\frac{a}{R}\\\tau &=kmaR\\\tau &=\frac{1}{2}(0,4)(4)(0,02)\\\tau &=0,016Nm\end{align*}
4. Dua buah benda diikat dengan tali yang dianggap tak bermassa kemudian talinya disangkutkan pada sebuah katrol seperti pada gambar.

Besar massa benda pertama 300 gram, besar massa benda kedua 500 gram, dan besar massa katrol 400 gram. Tentukanlah besar:
a. percepatan yang dialami benda;
b. tegangan tali;
Jawaban Fisika Pak Dimpun
a. percepatan yang dialami benda:\begin{align*}a&=\frac{\Delta mg }{\Sigma m+\frac{1}{2}M_k}\\a&=\frac{(0,5-0,3)10 }{0,5+0,3+\frac{1}{2}(0,4)}\\a&=2ms^{-2}\end{align*} b. tegangan tali; karena m1<m2 maka m2 turun dan m1 naik. \begin{align*}T_1&=m_1(g+a)\\T_1&=0,3(10+2)\\T_1&=3,6N \\T_2&=m_2(g-a)\\T_2&=0,5(10-2)\\T_2&=4,0N\end{align*} Lanjut soal Pengayaan Dinamika Rotasi [baca]
a. percepatan yang dialami benda;
b. tegangan tali;
Jawaban Fisika Pak Dimpun
a. percepatan yang dialami benda:\begin{align*}a&=\frac{\Delta mg }{\Sigma m+\frac{1}{2}M_k}\\a&=\frac{(0,5-0,3)10 }{0,5+0,3+\frac{1}{2}(0,4)}\\a&=2ms^{-2}\end{align*} b. tegangan tali; karena m1<m2 maka m2 turun dan m1 naik. \begin{align*}T_1&=m_1(g+a)\\T_1&=0,3(10+2)\\T_1&=3,6N \\T_2&=m_2(g-a)\\T_2&=0,5(10-2)\\T_2&=4,0N\end{align*} Lanjut soal Pengayaan Dinamika Rotasi [baca]







