Soal Pengayaan Dinamika Rotasi
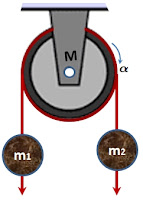
Soal 1. Sebuah katrol pejal bermassa (M) dan jari-jarinya (R) seperti pada gambar! Salah satu ujung tali tak bermassa dililitkan pada katrol, ujung tali yang lain digantungi beban m kg.

Saat beban dilepas, percepatan sudut katrol (α). Jika pada katrol ditempelkan plastisin A yang bermassa ½M, untuk menghasilkan percepatan sudut yang sama maka massa benda harus dijadikan... (Ikatrol = ½ MR2)
A. 3m/4
B. 3m/2
C. 2m
D. 3m
E. 4m
Penyelesaian Fisika: C
Keadaan awal:
gerak translasi (beban);

A. 3m/4
B. 3m/2
C. 2m
D. 3m
E. 4m
Penyelesaian Fisika: C
Keadaan awal:
gerak translasi (beban);

$\begin{align*} a&=\frac{\Sigma F}{m}\\a&=\frac{mg-T}{m}\\T&=mg-ma\\\\T&=mg-m(\alpha R)...(1)\end{align*}$
gerak rotasi (katrol):
gerak rotasi (katrol):
$\begin{align*} \Sigma \tau & = I\alpha \\ TR& = \frac12 MR^2\alpha \\ T& =\frac12 MR\alpha ...(2)\end{align*}$
Percepatan sudut katrol:
$\begin{align*} T&=mg-m(\alpha R)...(1)\\ T& =\frac12 MR\alpha ...(2)(-)\\ \hline mg&-m(\alpha R)=\frac12 MR\alpha \\mg&=\alpha \left [m+\frac12 M\right ]R\\\alpha&=\frac{mg}{\left [m+\frac12 M\right ]R} \end{align*}$
Keadaan setelah ditempeli Plastisin:
$\begin{align*} a'&=\frac{\Sigma F}{m'}\\a'&=\frac{m'g-T}{m'}\\T&=m'g-m'a'\\T&=m'g-m'(\alpha 'R)...(1)\end{align*}$
gerak rotasi (katrol):
$\begin{align*} \Sigma \tau & = I'\alpha '\\\Sigma \tau & = \left (I_k+I_p' \right )\alpha '\\ TR& = \left [\frac12 MR^2+\left ( \frac12M \right )R^2 \right ]\alpha' \\ T& =MR\alpha' ...(2)\end{align*}$
Percepatan sudut katrol:
$\begin{align*} T&=m'g-m'(\alpha 'R)...(1)\\ T& =MR\alpha' ......(2)(-)\\ \hline m'g&-m'\alpha 'R=MR\alpha '\\m'g&=\alpha '\left [m'+ M\right ]R\\\alpha '&=\frac{m'g}{\left [m'+ M\right ]R} \end{align*}$
percepatan sudut sama sebelum dan sesudah ditempeli plastisin;
$\begin{align*}\alpha &=\alpha '\\ \frac{m'g}{\left [m'+ M\right ]R} &= \frac{mg}{\left [m+ \frac12M\right ]R}\\\frac{m'}{m'+ M} &= \frac{m}{m+ \frac12M}\\mM + mm' &= mm'+\frac12Mm'\\mM &= \frac12 m'M\\m' &= 2m\end{align*}$
Soal 2. Sebuah sistem katrol berupa silinder pejal homogen yang dapat berotasi tanpa gesekan terhadap sumbunya yang tetap.
Percepatan sudut katrol:
$\begin{align*} T&=mg-m(\alpha R)...(1)\\ T& =\frac12 MR\alpha ...(2)(-)\\ \hline mg&-m(\alpha R)=\frac12 MR\alpha \\mg&=\alpha \left [m+\frac12 M\right ]R\\\alpha&=\frac{mg}{\left [m+\frac12 M\right ]R} \end{align*}$
Keadaan setelah ditempeli Plastisin:
$\begin{align*} a'&=\frac{\Sigma F}{m'}\\a'&=\frac{m'g-T}{m'}\\T&=m'g-m'a'\\T&=m'g-m'(\alpha 'R)...(1)\end{align*}$
gerak rotasi (katrol):
$\begin{align*} \Sigma \tau & = I'\alpha '\\\Sigma \tau & = \left (I_k+I_p' \right )\alpha '\\ TR& = \left [\frac12 MR^2+\left ( \frac12M \right )R^2 \right ]\alpha' \\ T& =MR\alpha' ...(2)\end{align*}$
Percepatan sudut katrol:
$\begin{align*} T&=m'g-m'(\alpha 'R)...(1)\\ T& =MR\alpha' ......(2)(-)\\ \hline m'g&-m'\alpha 'R=MR\alpha '\\m'g&=\alpha '\left [m'+ M\right ]R\\\alpha '&=\frac{m'g}{\left [m'+ M\right ]R} \end{align*}$
percepatan sudut sama sebelum dan sesudah ditempeli plastisin;
$\begin{align*}\alpha &=\alpha '\\ \frac{m'g}{\left [m'+ M\right ]R} &= \frac{mg}{\left [m+ \frac12M\right ]R}\\\frac{m'}{m'+ M} &= \frac{m}{m+ \frac12M}\\mM + mm' &= mm'+\frac12Mm'\\mM &= \frac12 m'M\\m' &= 2m\end{align*}$
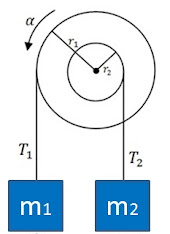
Soal 2. Sebuah sistem katrol berupa silinder pejal homogen yang dapat berotasi tanpa gesekan terhadap sumbunya yang tetap.
Massa beban m1 = m, massa katrol M = 2m, massa beban m2 = 3m dan diameter katrol d. Jika percapatan gravitasi g dan sistem bergerak tanpa pengaruhi gaya luar, percepatan sudut rotasi katrol sebesar...
A. 2g/5d
B. 3g/5d
C. 4g/5d
D. 6g/5d
E. g/d
Penyelesaian Fisika: C
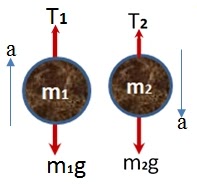
gerak translasi benda m1
$\begin{align*} a&=\frac{\Sigma F}{m_1}\\a&=\frac{T_1-m_1g}{m_1}\\T_1&=m_1g+m_1a\end{align*}$
A. 2g/5d
B. 3g/5d
C. 4g/5d
D. 6g/5d
E. g/d
Penyelesaian Fisika: C
gerak translasi benda m1
$\begin{align*} a&=\frac{\Sigma F}{m_1}\\a&=\frac{T_1-m_1g}{m_1}\\T_1&=m_1g+m_1a\end{align*}$

gerak translasi benda m2,
$\begin{align*} a&=\frac{\Sigma F}{m_2}\\a&=\frac{m_2g-T_2}{m_2}\\T_2&=m_2g-m_2a\end{align*}$
gerak rotasi katrol:
$\begin{align*} a&=\frac{\Sigma F}{m_2}\\a&=\frac{m_2g-T_2}{m_2}\\T_2&=m_2g-m_2a\end{align*}$
gerak rotasi katrol:
$\small \begin{align*} \Sigma \tau & = I\alpha \\(T_2-T_1)R& = \frac12MR^2\left ( \frac{a}{R} \right )\\ (m_2g-m_2a) &-(m_1g+m_1a)= \frac12Ma\\ (m_2-m_1)g&-(m_2+m_1)a =\frac12Ma\\a=&\frac{(m_2-m_1)g}{(m_2+m_1)+\frac12M}\end{align*}$
Percepatan sudut katrol:
$\begin{align*} \alpha & = \frac aR \\& = \frac{\frac{(m_2-m_1)g}{(m_2+m_1)+\frac12M}}{\frac{d}{2}}\\ &=\frac{(3m-m)g}{(3m+m)+\frac12(2m)}\left (\frac{2}{d} \right )\\ &=\frac{4g}{5d}\end{align*}$
Soal 3. Pada sebuah roda gila yang momen inersianya 4,0 kg m2 dikerjakan momen 50 mN. Enam sekon setelah mulai berotasi pada kecepatan sudut 40 rad/s roda gila telah menempuh putaran sejauh...
A. 225 rad
B. 315 rad
C. 465 rad
D. 545 rad
E. 3053 rad
Penyelesaian Fisika: C
Percepatan sudut roda gila:
$\begin{align*} \tau &=I\alpha\\\alpha &= \frac{\tau }{I} \\&= \frac{50}{4} = 12,5\, rad.s^{-2}\end{align*}$
Putaran selama 6 sekon:
$\begin{align*} \Delta \theta &= \omega _ot+\frac{1}{2}\alpha t^2 \\&= 40(6) + \frac{1}{2} (12,5 )(6 )^2 \\&= 465\textrm{ rad}\end{align*}$
Percepatan sudut katrol:
$\begin{align*} \alpha & = \frac aR \\& = \frac{\frac{(m_2-m_1)g}{(m_2+m_1)+\frac12M}}{\frac{d}{2}}\\ &=\frac{(3m-m)g}{(3m+m)+\frac12(2m)}\left (\frac{2}{d} \right )\\ &=\frac{4g}{5d}\end{align*}$
Soal 3. Pada sebuah roda gila yang momen inersianya 4,0 kg m2 dikerjakan momen 50 mN. Enam sekon setelah mulai berotasi pada kecepatan sudut 40 rad/s roda gila telah menempuh putaran sejauh...
A. 225 rad
B. 315 rad
C. 465 rad
D. 545 rad
E. 3053 rad
Penyelesaian Fisika: C
Percepatan sudut roda gila:
$\begin{align*} \tau &=I\alpha\\\alpha &= \frac{\tau }{I} \\&= \frac{50}{4} = 12,5\, rad.s^{-2}\end{align*}$
Putaran selama 6 sekon:
$\begin{align*} \Delta \theta &= \omega _ot+\frac{1}{2}\alpha t^2 \\&= 40(6) + \frac{1}{2} (12,5 )(6 )^2 \\&= 465\textrm{ rad}\end{align*}$
Momen inersia sistem katrol adalah I=1,90 kg m2, m1= 4 kg , m2= 2,5 kg sedangkan r1=50 cm dan r2=20 cm, g=10 m/s2. Tentukan :
Gerak Translasi benda m1:
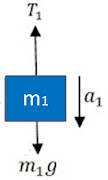
$\begin{align*}a_1&=\frac{\Sigma F}{m_1}\\a_1&=\frac{m_1g-T_1}{m_1}\\T_1&=m_1g-m_1a_1\\T_1&=m_1g-m_1(\alpha r_1)\end{align*}$
Gerak Translasi benda m2: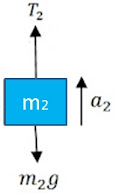
$\begin{align*}a_2&=\frac{\Sigma F}{m_2}\\a_2&=\frac{T_2-m_2g}{m_2}\\T_2&=m_2g+m_2a_2\\T_2&=m_2g+m_2(\alpha r_2)\end{align*}$
Gerak Rotasi Katrol:
$\Sigma \tau =I\alpha \\(T_1r_1-T_2r_2)=I\alpha \\(m_1g-m_1\alpha r_1)r_1-(m_2g+m_2\alpha r_2)r_2=I\alpha \\m_1gr_1-m_2gr_2 -m_1\alpha r^2_1-m_2\alpha r^2_2=I\alpha\\m_1gr_1-m_2gr_2=I\alpha +m_2\alpha r^2_2+m_1\alpha r^2_1\\\alpha =\frac{(m_1r_1-m_2r_2)g}{I +m_1 r^2_1+m_2 r^2_2}$
Kita masukkan angkanya...
Tegangan tali (1):
$\begin{align*}T_1&=m_1g-m_1(\alpha r_1)\\&=4(10)-4(5)(0,5)\\&=30N\end{align*}$
Tegangan tali (2):
$\begin{align*}T_2&=m_2g+m_2(\alpha r_2)\\&=2,5(10)-2,5(5)(0,2)\\&=27,5N\end{align*}$
- Percepatan sudut sistem katrol!
- Tegangan tali T1 dan T2.
Gerak Translasi benda m1:

$\begin{align*}a_1&=\frac{\Sigma F}{m_1}\\a_1&=\frac{m_1g-T_1}{m_1}\\T_1&=m_1g-m_1a_1\\T_1&=m_1g-m_1(\alpha r_1)\end{align*}$
Gerak Translasi benda m2:

$\begin{align*}a_2&=\frac{\Sigma F}{m_2}\\a_2&=\frac{T_2-m_2g}{m_2}\\T_2&=m_2g+m_2a_2\\T_2&=m_2g+m_2(\alpha r_2)\end{align*}$
Gerak Rotasi Katrol:

$\Sigma \tau =I\alpha \\(T_1r_1-T_2r_2)=I\alpha \\(m_1g-m_1\alpha r_1)r_1-(m_2g+m_2\alpha r_2)r_2=I\alpha \\m_1gr_1-m_2gr_2 -m_1\alpha r^2_1-m_2\alpha r^2_2=I\alpha\\m_1gr_1-m_2gr_2=I\alpha +m_2\alpha r^2_2+m_1\alpha r^2_1\\\alpha =\frac{(m_1r_1-m_2r_2)g}{I +m_1 r^2_1+m_2 r^2_2}$
Kita masukkan angkanya...
- I=1,90 kg m2,
- m1= 4 kg
- m2= 2,5 kg
- r1=50 cm
- r2=20 cm.
Tegangan tali (1):
$\begin{align*}T_1&=m_1g-m_1(\alpha r_1)\\&=4(10)-4(5)(0,5)\\&=30N\end{align*}$
Tegangan tali (2):
$\begin{align*}T_2&=m_2g+m_2(\alpha r_2)\\&=2,5(10)-2,5(5)(0,2)\\&=27,5N\end{align*}$