SOAL PENYELESAIAN UJI KOMPETENSI 1.2 HALAMAN 30 BUKU GRAFINDO KELAS 11

Uji kompetensi 1.2 halaman 30 buku Siswa Aktif dan Kreatif Belajar Fisika kelas 11 Penerbit Grafindo.

Soal no. 1. Perhatikan gambar berikut:

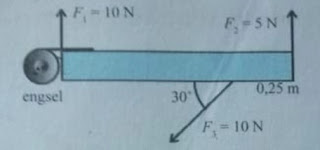
Jika diketahui panjang batang adalah 1 m, tentukan resultan momen gaya yang bekerja pada batang dengan pusat torsi engsel.
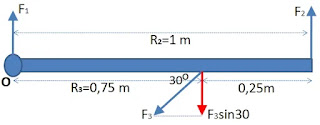
Penyelesaian Fisika:

Kita sepakati dulu, arah momen gayanya:

• searah putaran jam: positip
• berlawanan putaran jam: negatip

\begin{align*} \Sigma  \tau _o&=F_1R_1+F_2R_2+F_3R_3\\\Sigma  \tau _o&=10(0)+5(1)-20(0,5)(0,75)\\\Sigma  \tau _o&=0+5-7,5\\\Sigma  \tau _o&=-2,5\, Nm\\&\textrm{Berlawanan putaran jarum jam}\end{align*}

---

Soal no. 2. Sebuah batang panjangnya l, massa m, dan sumbu rotasi terletak 1/3l dari ujung kiri batang dan tegak lurus terhadap batang. Tentukan besarnya momen inersia batang terhadap sumbu rotasinya.

Penyelesaian Fisika:
Sumbu putar bergeser sejauh $x=\frac{1}{2}l-\frac {1}{3}l=\frac {1}{6}l$
konsep teorema pergeseran sumbu putar:\begin{align*} I&=I_{pm}+mx^2\\I_{pm}&=\frac{1}{3}ml^2\\&maka:\\I&=I_{pm}+mx^2\\I&=\frac{1}{3}ml^2+m\left (\frac{1}{6}l  \right )^2\\I&=\frac{1}{3}ml^2+\frac{1}{36}ml^2\\I&=\frac{4}{36}ml^2=\frac{1}{9}ml^2\end{align*}

---

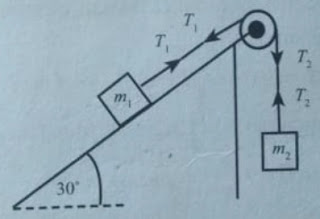
Soal no. 3. Perhatikan gambar berikut:

Dua balok m₁=m₂=0,5 kg. Balok m₁ berada pada bidang miring licin. Diketahui pula kontrol berbentuk silinder berongga massanya 0,25 kg. Jika $g =10ms^{-2}$, tentukanlah perbandingan tegangan tali T₁ dan T₂
Penyelesaian Fisika:

Tinjau benda m₁, posisi naik: \begin{align*} \Sigma F=ma&\\T_1-m_1g\sin 30=m_1a&\\T_1-0,5(10)(0,5)=0,5a&\\T_1=0,5a+2,5&...(1)\end{align*}Tinjau benda m₂, posisi turun: \begin{align*} \Sigma F=ma&\\m_2g-T_2=m_2a&\\0,5(10)-T_2=0,5a&\\T_2=5-0,5a&...(2)\end{align*}Tinjau katrol:\begin{align*} \Sigma \tau =I\alpha &=I\frac{a}{R}&\\(T_2-T_1)R&=I\frac{a}{R}&\\\left ((5-0,5a)-(0,5a+0,25)  \right )R&=mR^2\frac{a}{R}\\2,5-a&=0,25a\\1,25a&=2,5\\a&=2ms^{-2}\end{align*}Perbandingan T₁ terhadap T₂:\begin{align*} \frac{T_1}{T_2}&=\frac{0,5a+2,5}{5-0,5a}\\\frac{T_1}{T_2}&=\frac{0,5(2)+2,5}{5-0,5(2)}\\\frac{T_1}{T_2}&=\frac{3}{3,75}=0,8\end{align*}

---

Soal no. 4.Tentukan besar energi kinetik total dari sebuah slinder berongga yang sedang menggelinding pada sebuah bidang miring dengan kelajuan konstan 4 m/s jika diketahui massanya 20 kg, jari-jari lingkaran dalamnya 1m dan jari-jari lingkaran luarnya 2m. Penyelesaian Fisika: Momen inersia slinder berongga: \begin{align*} I&=\frac{1}{2}m(R_1^2+R_2^2)\\I&=\frac{1}{2}(20)(1^2+2^2)\\ I&=50Nm\end{align*} Energi total:\begin{align*} E&=Ek_t+Ek_r\\E&=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\Rightarrow \omega =\frac {v}{R}\\E&=\frac{1}{2}mv^2+\frac{1}{2}I\left ( \frac {v}{R_2} \right )^2\\E&=\frac{1}{2}20(4)^2+\frac{1}{2}(50)\left ( \frac {4}{2} \right )^2\\E&=160+100=260J\end{align*}