Soal dan Penyelesaian Ujian Akhir Semester Fisika Kelas 12
Soal 1: Sebuah balok diukur menggunakan jangka sorong memiliki panjang, lebar, dan tinggi seperti ditunjukkan pada gambar.

Volume balok tersebut sesuai dengan kaidah angka penting adalah...
A. 1,130 cm3
B. 1,13 cm3
C. 1,1 cm3
D. 1,2 cm3
E. 1,5 cm3
Penyelesaian Fisika: C
Pembacaan jangka sorong:
$\begin{align*}p&=1,82\textrm{ cm}\\l&=0,46\textrm{ cm}\\t&=1,35\textrm{ cm}\, \, \, \times\\\hline V &= p\times l\times t\\&=1,13022\mathrm{ \, cm^3}\\& = 1,1\mathrm{ \, cm^3}\\&\textrm{ 2 angka penting}\end{align*}$
Soal 2: Soal UNBK Fisika SMA 2019
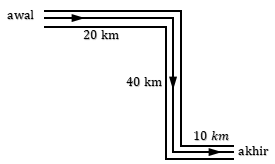
Seorang mengendarai motor dengan rute seperti yang ditunjukkan pada gambar berikut.
A. 1,130 cm3
B. 1,13 cm3
C. 1,1 cm3
D. 1,2 cm3
E. 1,5 cm3
Penyelesaian Fisika: C
Pembacaan jangka sorong:
- Panjang = 1,82cm (3 angka penting)
- Lebar = 0,46cm (2 angka penting)
- Tinggi = 1,35cm (3 angka penting)
$\begin{align*}p&=1,82\textrm{ cm}\\l&=0,46\textrm{ cm}\\t&=1,35\textrm{ cm}\, \, \, \times\\\hline V &= p\times l\times t\\&=1,13022\mathrm{ \, cm^3}\\& = 1,1\mathrm{ \, cm^3}\\&\textrm{ 2 angka penting}\end{align*}$
Soal 2: Soal UNBK Fisika SMA 2019
Seorang mengendarai motor dengan rute seperti yang ditunjukkan pada gambar berikut.

Besar perpindahan yang ditempuh orang tersebut adalah...
A. 30 km
B. 40 km
C. 50 km
D. 60 km
E. 70 km
Penyelesaian Fisika: C
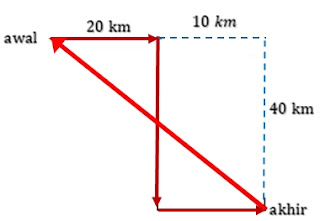
Perhatikan gambar !
A. 30 km
B. 40 km
C. 50 km
D. 60 km
E. 70 km
Penyelesaian Fisika: C
Perhatikan gambar !

Perpindahan adalah jarak antara posisi awal dan posisi akhir. Dengan dalil Pithagoras, jarak antara posisi awal dan posisi akhir adalah:
$\begin{align*}r&=\sqrt{(20+10)^2+40^2}\\&=50\textrm{ km}\end{align*}$
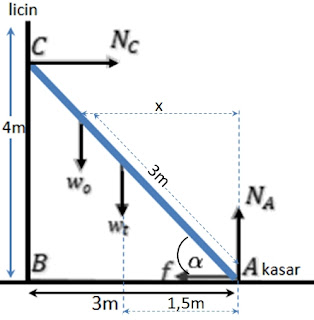
Soal 3: Perhatikan gambar berikut !
$\begin{align*}r&=\sqrt{(20+10)^2+40^2}\\&=50\textrm{ km}\end{align*}$
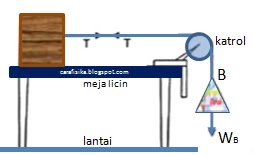
Soal 3: Perhatikan gambar berikut !

Diketahui percepatan sistem adalah $a_{sistem}$, percepatan gravitasi adalah $g$, dan tegangan tali adalah $T$. Besar percepatan balok A adalah...
$\begin{align*}&A.\ a_A = \frac{m_B.g}{m_A}\\&B.\ a_A = \frac{m_B.g - T}{m_A}\\&C.\ a_A = \frac{m_A.m_B.g}{m_A + m_B}\\&D.\ a_A = \frac{m_B.g}{m_A + m_B}\\&E.\ a_A = \frac{T - m_B.g}{m_A}\end{align*}$
Penyelesaian Fisika: D
Percepatan benda A sama dengan percepatan benda B.
$\begin{align*}a&=\frac{\Sigma F}{m}\\&=\frac{W_B}{m_A+m_B}\\& = \frac{m_B.g}{m_A+m_B}\end{align*}$
Soal 4: Satelit Helios 1 dan Helios 2 mengorbit Bumi dengan perbandingan jari-jari orbitnya $4 : 9$ serta perbandingan massa Helios 1 dan Helios 2 adalah $4 : 9$. Jika lintasan orbit satelit tersebut melingkar, maka perbandingan periode satelit Helios 1 dan Helios 2 adalah...
$\begin{align*}&A.\ a_A = \frac{m_B.g}{m_A}\\&B.\ a_A = \frac{m_B.g - T}{m_A}\\&C.\ a_A = \frac{m_A.m_B.g}{m_A + m_B}\\&D.\ a_A = \frac{m_B.g}{m_A + m_B}\\&E.\ a_A = \frac{T - m_B.g}{m_A}\end{align*}$
Penyelesaian Fisika: D
Percepatan benda A sama dengan percepatan benda B.
$\begin{align*}a&=\frac{\Sigma F}{m}\\&=\frac{W_B}{m_A+m_B}\\& = \frac{m_B.g}{m_A+m_B}\end{align*}$
Soal 4: Satelit Helios 1 dan Helios 2 mengorbit Bumi dengan perbandingan jari-jari orbitnya $4 : 9$ serta perbandingan massa Helios 1 dan Helios 2 adalah $4 : 9$. Jika lintasan orbit satelit tersebut melingkar, maka perbandingan periode satelit Helios 1 dan Helios 2 adalah...
A. 4 : 9
B. 4 : 27
C. 8 : 27
D. 27 : 4
E. 27 : 8
Penyelesaian Fisika: C
$\left(\frac{T_1}{T_2} \right)^2 = \left(\frac{R_1}{R_2} \right)^3$
$\begin{align*}\left(\frac{T_1}{T_2} \right)^2 = \left(\frac{4}{9} \right)^3\end{align*}$
$\begin{align*}\left(\frac{T_1}{T_2} \right)^2 = \left(\frac{4}{9} \right)^2\left(\frac{4}{9} \right)\end{align*}$
$\begin{align*}\left(\frac{T_1}{T_2} \right) = \left(\frac{4}{9} \right)\left(\frac{2}{3} \right)\end{align*}$
$\begin{align*}\frac{T_1}{T_2} =\frac{8}{27}\end{align*}$
Soal 5: Perhatikan gambar berikut !

B. 4 : 27
C. 8 : 27
D. 27 : 4
E. 27 : 8
Penyelesaian Fisika: C
$\left(\frac{T_1}{T_2} \right)^2 = \left(\frac{R_1}{R_2} \right)^3$
$\begin{align*}\left(\frac{T_1}{T_2} \right)^2 = \left(\frac{4}{9} \right)^3\end{align*}$
$\begin{align*}\left(\frac{T_1}{T_2} \right)^2 = \left(\frac{4}{9} \right)^2\left(\frac{4}{9} \right)\end{align*}$
$\begin{align*}\left(\frac{T_1}{T_2} \right) = \left(\frac{4}{9} \right)\left(\frac{2}{3} \right)\end{align*}$
$\begin{align*}\frac{T_1}{T_2} =\frac{8}{27}\end{align*}$
Soal 5: Perhatikan gambar berikut !

Gambar di atas menunjukkan seorang ibu mendorong kereta belanja di atas bidang datar licin dengan gaya $F$ sehingga berjalan dalam selang waktu $t$. Tabel berikut ini berisi data-data tentang massa (M), gaya dorong (F), dan waktu (t):


Berdasarkan tabel di atas, maka urutan data yang menghasilkan usaha mulai dari terkecil adalah...
A. (1) - (2) - (3) - (4)
B. (1) - (3) - (4) - (2)
C. (2) - (4) - (3) - (1)
D. (3) - (1) - (2) - (4)
E. (4) - (2) - (1) - (3)
Penyelesaian Fisika: E
$\begin{align*}s&=v_ot+\frac{1}{2}at^2\Rightarrow v_o=0\\s&=\frac{1}{2}\frac{F}{m}t^2\times \frac{F}{F}\\Fs&=\frac{\left (Ft \right )^2}{2m}\Rightarrow W=Fs\\W&=\frac{\left (Ft \right )^2}{2m}\end{align*}$
Nomor 1:
$W = \frac{(25.4)^2}{2.40} = 125\ J$
Nomor 2:
$W = \frac{(30.2)^2}{2.30} = 60\ J$
Nomor 3:
$W = \frac{(20.10)^2}{2.25} = 800\ J$
Nomor 4:
$W = \frac{(10.5)^2}{2.50} = 25\ J$
Urutan usaha dari terkecil adalah: (4) - (2) - (1) - (3)
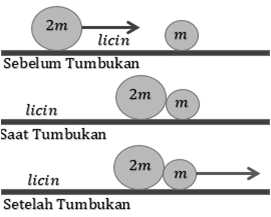
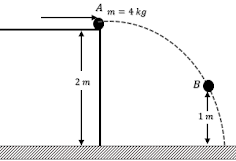
Soal 6: Sebuah bola pejal dengan massa $4\ kg$ terletak di ujung lemari kemudian didorong mendatar sehingga kecepatannya $2\ m.s^{-1}$ pada saat lepas dari tepi atas lemari seperti tampak pada gambar di bawah.
A. (1) - (2) - (3) - (4)
B. (1) - (3) - (4) - (2)
C. (2) - (4) - (3) - (1)
D. (3) - (1) - (2) - (4)
E. (4) - (2) - (1) - (3)
Penyelesaian Fisika: E
$\begin{align*}s&=v_ot+\frac{1}{2}at^2\Rightarrow v_o=0\\s&=\frac{1}{2}\frac{F}{m}t^2\times \frac{F}{F}\\Fs&=\frac{\left (Ft \right )^2}{2m}\Rightarrow W=Fs\\W&=\frac{\left (Ft \right )^2}{2m}\end{align*}$
Nomor 1:
$W = \frac{(25.4)^2}{2.40} = 125\ J$
Nomor 2:
$W = \frac{(30.2)^2}{2.30} = 60\ J$
Nomor 3:
$W = \frac{(20.10)^2}{2.25} = 800\ J$
Nomor 4:
$W = \frac{(10.5)^2}{2.50} = 25\ J$
Urutan usaha dari terkecil adalah: (4) - (2) - (1) - (3)
Soal 6: Sebuah bola pejal dengan massa $4\ kg$ terletak di ujung lemari kemudian didorong mendatar sehingga kecepatannya $2\ m.s^{-1}$ pada saat lepas dari tepi atas lemari seperti tampak pada gambar di bawah.

Percepatan gravitasi adalah $10\ m.s^{-2}$, maka energi mekanik partikel pada saat benda berada pada ketinggian $1\ m$ dari tanah sebesar...
A. 40 J
B. 48 J
C. 80 J
D. 88 J
E. 96 J
Penyelesaian Fisika: D
Energi mekanik sistem adalah tetap.
$\begin{align*}EM_B = EM_A &= \frac12mv_A^2 + mgh_A\\EM_B &= \frac12.4.2^2 + 4.10.2\\EM_B &= 8 + 80\\EM_B &= 88\ J\end{align*}$
Soal 7: Berikut adalah grafik hubungan kecepatan $(v)$ terhadap waktu $(t)$ dua mobil A dan B yang bergerak dari posisi dan lintasan yang sama.

A. 40 J
B. 48 J
C. 80 J
D. 88 J
E. 96 J
Penyelesaian Fisika: D
Energi mekanik sistem adalah tetap.
$\begin{align*}EM_B = EM_A &= \frac12mv_A^2 + mgh_A\\EM_B &= \frac12.4.2^2 + 4.10.2\\EM_B &= 8 + 80\\EM_B &= 88\ J\end{align*}$
Soal 7: Berikut adalah grafik hubungan kecepatan $(v)$ terhadap waktu $(t)$ dua mobil A dan B yang bergerak dari posisi dan lintasan yang sama.

Dari pernyataan-pernyataan berikut:
A. (1) dan (2)
B. (1) dan (3)
C. (2) dan (3)
D. (3) dan (4)
Penyelesaian Fisika: C
Mobil A:
$\begin{align*}v &= v_o + at\\60 &= 0 + a.40\\a &= 1,5\ m/s^2\\\\s &= v_ot + \frac12at^2\\S &= 0.40 + \frac12.1,5.40^2\\S &= 1200\ m\end{align*}$
Mobil B:
$\begin{align*}v &= v_o + at\\60 &= 36 + 40a\\a &= \frac{24}{40} = 0,6\ m/s^2\\\\s &= v_ot + \frac12at^2\\ &= 36.40 + \frac12.0,6.40^2\\ &= 1440 + 480 = 1920\ m\end{align*}$
Kesimpulan:
Lanjut soal nomor - 8
- Mobil A dan B sama-sama berhenti pada detik ke-60.
- Percepatan mobil A lebih besar dibanding percepatan mobil B.
- Mobil A menempuh perjalanan lebih dekat dari pada mobil B.
- Mobil A dan B bertemu setelah bergerak 40 sekon.
A. (1) dan (2)
B. (1) dan (3)
C. (2) dan (3)
D. (3) dan (4)
Penyelesaian Fisika: C
Mobil A:
$\begin{align*}v &= v_o + at\\60 &= 0 + a.40\\a &= 1,5\ m/s^2\\\\s &= v_ot + \frac12at^2\\S &= 0.40 + \frac12.1,5.40^2\\S &= 1200\ m\end{align*}$
Mobil B:
$\begin{align*}v &= v_o + at\\60 &= 36 + 40a\\a &= \frac{24}{40} = 0,6\ m/s^2\\\\s &= v_ot + \frac12at^2\\ &= 36.40 + \frac12.0,6.40^2\\ &= 1440 + 480 = 1920\ m\end{align*}$
Kesimpulan:
- Mobil A dan mobil B mengalami GLBB dipercepat, sehingga tidak berhenti. Pernyataan (1) salah.
- Percepatan mobil A lebih besar dari percepatan mobil B. Pernyataan (2) benar.
- Setelah 40s jarak tempuh mobil A lebih pendek dari jarak tempuh mobil B. Pernyataan (3) benar.
- Pada saat t = 40s mobil A menempuh jarak 1200m sedangkan mobil B menempuh jarak 1920m, dengan demikian mereka tidak bertemu.
Lanjut soal nomor - 8