Sebuah benda bermassa m’ yang terletak pada jarak r dari pusat massa benda bermassa m memiliki Energi Potensial dengan persamaan : \[ Ep = - G \frac{m_{1}m_{2}}{R}\] Bila massa m’ terletak dititik p maka potensial gravitasi di titik p yang dialami oleh massa m’ dapat ditentukan sebagai berikut : \[ V = - G \frac{m}{R}\] V = potensial gravitasi pada jarak r dari massa m m = massa benda
R = jarak tempat yang mengalami potensial gravitasi ke benda.
Potensial gravitasi merupakan besaran skalar, karena itu potensial yang disebabkan oleh berapa benda bermassa merupakan jumlah aljabar dari potensial gravitasi masing-masing benda bermassa itu, Jadi :
\[V_{t}=V_{1}+V_{2}+V_{3}+..+V_{2}\]Usaha(W) yang dilakukan untuk mengangkut, massa m dari satu titik ke titik lain ( misalnya dari A ke B ) lewat sembarang lintasan sama dengan massa benda itu kali beda potensial antara kedua titik itu.
\[W_{AB}=m(V_{B}-V_{A})\]
HUKUM KEKEKALAN ENERGI
Untuk gerakan benda dalam medan gravitasi yang tidak sama kekuatan di semua titik, hendaknya dipecahkan dengan perhitungan potensial gravitasi atau tenaga potensial gravitasi. Jika gaya-gaya gesekan diabaikan, dasar persangkutannya hanyalah kekekalan energi, yaitu :
\[E_{k}+E_{p}=\textrm{konstan}\]\[E_{k1}+E_{p1}=E_{k2}+E_{p2}\]Disini pembicaraan akan kita batasi hanya mengenai gerakan massa m dalam medan gravitasi yang ditimbulkan oleh titik tunggal yang tetap atau bola homogen bermassa m. Sehingga :
$ E_{k}= \frac{1}{2}mv^{2}$ dan $E_{p} = - G \frac{M.m}{R}$
Akhirnya kita dapatkan bahwa :
$\frac{1}{2}mv_{1}^{2} - G \frac{M.m}{R_{1}}= \frac{1}{2}mv_{2}^{2} - G \frac{M.m}{R_{2}}$
KELAJUAN LEPAS
Sebuah benda yang dilemparkan lurus ke atas dari permukaan bumi hanya dapat naik sampai jarak tertentu pada waktu energi Kinetik benda sama dengan nol, kemudian akan kembali lagi ke permukaan bumi. Jika suatu benda dilemparkan dari permukaan bumi dengan energi kinetik yang besarnya sama dengan energi potensial dipermukaan bumi, maka energi totalnya sama dengan nol.
Ini berarti benda bergerak ke jauh tak terhingga atau lepas dari bumi. Kelajuan awal agar ini terjadi disebut kelajuan lepas, dan dapat ditentukan dengan persamaan :
\[\frac{1}{2}mv^{2} = G \frac{M.m}{R_{2}}\]
atau :
\[ v = \sqrt{2gR}\]v = kelajuan lepas R = jari-jari bumi
g = percepatan gravitasi bumi.
GERAKAN PLANET
Menurut Keppler ( hukum Keppler ), perbandingan antara T2 dari gerakan planet yang mengelilingi matahari terhadap R3 adalah konstan. \[ \frac{T^{2}}{R^{3}} = konstan\] T = perioder = jari-jari lintasan
\[ \left ( \frac{T_{1}}{T_{2}} \right )^{2}=\left ( \frac{R_{1}}{R_{2}} \right )^{3}\]
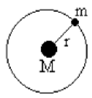Dan dari gerak melingkar beraturan dapat kita peroleh : $v=\frac{2\pi R}{T}$ Karena planet bergerak pada lintasan yang tetap maka terdapat gaya centripetal yang mempertahankan planet tetap pada lintasannya. \[F = G\frac{m_{1}m_{2}}{R^{2}}\]Gaya sentripetal dalam hal ini adalah gaya gravitasi yang dialami oleh planet yang disebabkan oleh matahari.
Bila massa planet m dan massa planet m dan massa matahari M maka gaya gravitasi antara planet dan matahari pada jarak R, adalah :
Gaya ini merupakan gaya centripetal. Bila selama mengitari matahari planet bergerak dengan laju tetap sebesar v, maka dapat dinyatakan bahwa : \[G\frac{M.m}{R^{2}}=\frac{mv^{2}}{R}\]\[ G\frac{M}{R^{2}}=\frac{v^{2}}{R}\]\[ v=\sqrt{G\frac{M}{R}}\]Jika planet bergerak dengan kelajuan sudut w maka dapat dinyatakan suatu persamaan dalam bentuk :
\[ \omega ^{2}= G\frac{M}{R^{3}}\]$\omega $ = kelajuan sudut
M = massa matahari
R = jari-jari lintasan
