Pembahasan soal SBMPTN Fisika 2017 ini dapat digunakan sebagai gambaran konsep apa saja muncul pada tahun tersebut.
16. Perhatikanlah grafik berikut ini.
Sebuah benda bergerak pada lintasan lurus dengan posisi setiap saat digambarkan seperti grafik di atas. Penyataan yang benar mengenai grafik di atas adalah
A. Kecepatan rata-rata pada selang waktu 0.5≤ t≤ 2 detik adalah 3 m/s
B. Kecepatan rata-rata pada selang waktu 1≤ t ≤3.5 detik adalah 0 m/s
C. Kecepatan rata-rata pada selang waktu 3.5≤ t≤ 5 detik adalah 10 m/s
D. Kecepatan saat t = 4 detik adalah 10 m/s
E. Kecepatan saat t = 1 detik adalah 4 m/s
Jawaban Fisika dari Pak Dimpun: E
Perhatikanlah keadaan grafik untuk tiap selang waktu pada soal.
- Selang waktu 0s-1.5s benda begerak dengan kecepatan konstan dengan laju \[\\ v_{(0-1.5)}=\frac{\Delta x}{\Delta t} \\\\ v_{(0-1.5)}=\frac{6-0}{1.5-0} \\\\ v_{(0-1.5)}=4 ms^{-1}\]
- Selang waktu 3.5 s-5s bergerak dengan kecepatan konstan dengan laju \[\\v_{(3.5-5)}=\frac{\Delta x}{\Delta t}\\\\ v_{(3.5-5)}=\frac{16-6}{5-3.5}ms^{-1}\\\\ v_{(3.5-5)}=\frac{20}{3} ms^{-1}\]
17. Sebuah lemari besi dengan berat 300N (awalnya dalam keadaan diam) ditarik dengan sebuah gaya dengan arah θ terhadap garis mendatar (cosθ = 3/5). Apabila koefisien statis dan kinetis benda dengan lantai beturut-turut 0.5 dan 0.4, gaya gesek kinetik yang bekerja pada lemari 72N dan percepatan gravitasi 10 m/s2, percepatan lemari besi dan gaya tarik yang bekerja pada lemari adalah
A. 18/30 m/s2 dan 90N
B. 18/30 m/s2 dan 150N
C. 18/30 m/s2 dan 210N
D. 0 m/s2 dan 150N
E. 0 m/s2 dan 90N
Jawaban Fisika dari Pak Dimpun: B
Sketsa soal digambarkan sebagai berikut ini.
- Gaya normal N benda. \[f_{k}=\mu _{K}.N\\\\N=\frac{f_{k}}{\mu _{k}}\\\\N=\frac{72}{0.4}=180N\]
- Gaya F dapat dihitung dari komponen gaya arah vertikal (y). \[\\ Fsin\theta =W-N\\\\ F=\frac{W-N}{sin\theta }\\\\ F=\frac{300-180}{4/5}=150N\]
- Pecepatan benda dapat dihitung dari komponen gaya dalam arah horizontal (x). \[\\\Sigma F_{x}=ma\\\\ Fcos\theta -f_{k}=ma\\\\ a=\frac{150(3/5)-72}{30}ms^{-2}\\\\a=18/30 ms^{-2}\]
18. Pada sebuah bidang datar licin, sebuah kelereng bergerak dari kiri sepanjang sumbu-x menuju titik pusat O (0,0) dengan laju v. Kelereng tersebut menumbuk kelereng kedua dengan massa sama yang diam di titik O. Jika kecepatan kelereng pertama dan kedua setelah tumbukan v1' dan v2’ dengan arah θ dan 330o terhadap sumbu-x dan selisih v2' terhadap v1' adalah $\frac{(\sqrt{3}-1)v}{2}$ maka nilai θ adalah
A. 30o
B. 45o
C. 60o
D. 180o
E. 270o
Jawaban Fisika dari Pak Dimpun: C
Sketsa digambarkan adalah sebagai berikut.
Seutas tali yang tipis disambung dengan tali yang tebal, kemudian diikatkan pada sebuah tembok yang kokoh seperti pada gambar di atas. Jika pada salah satu ujung tali yang tipis diberi gangguan, terjadi gelombang yang merambat ke kanan. Pada saat di A
SEBAB
- \[\\ v_{2}^{'}-v_{1}^{'}=\frac{\sqrt{3}}{2}v-\frac{v}{2} \\\\\mathrm{diperoleh.....}\\\\v_{2}'=\frac{\sqrt{3}}{2}v\\\\ v_{1}'=\frac{v}{2}\]
- Hukum kekekalan momentum dalam arah-y adalah \[\\m_{1}v_{1y}+m_{2}v_{2y}=m_{1}v_{1}'sin\theta -m_{2}v_{2}'sin30^{o}\\\\ 0=m_{1}v_{1}'sin\theta -m_{2}v_{2}'sin30^{o}\\\\m_{1}=m_{2}\\\\v_{1}'sin\theta =v_{2}'sin30^{o} \\\\ \frac{v}{2}sin\theta =\frac{\sqrt{3}}{2}v\left ( \frac{1}{2} \right )\\\\ sin\theta =\frac{\sqrt{3}}{2}\\\\\theta =60^{o}\]
19. Elevator pada sebuah bangunan dirancang sehingga dapat mengangkat beban 2000 kg (termasuk massa elevator) dengan percepatan 1.5 m/s2. Untuk alasan teknis dan keamanan, luas penampang kawat yang digunakan 2.3 x 10-5 meter persegi dan besarnya regangan diisyaratkan harus lebih kecil 8 x 10-4). Jika percepatan gravitasi 10 m/s2, nilai modulus Young kabel adalah
A. 2.5 x 1010 N/m2
B. 2.7 x 1011 N/m2
C. 8.0 x 1011 N/m2
D. 1.0 x 1012 N/m2
E. 1.25 x 1012 N/m2
- Tengan tali pada kawat elevator.
\[\\\Sigma F=ma\\\\ T-W=ma\\\\ T=mg+ma\\\\T=2000(10)+2000(1.5)\\\\T=23.10^{3}N\]
- Modulus Young
\[\\E=\frac{\sigma }{e}\\\\ E=\frac{T}{A.e}\\\\ E=\frac{23.10^{3}}{(2.3\times 10^{-5}).(8.10^{-4})}\\\\E=1.25\times 10^{12}Nm^{-2}\]
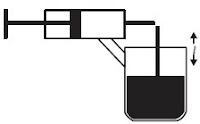
20. Perhatikanlah gambar di bawah ini.
Semprotan nyamuk tersusun atas pipa vertikal yang tercelup dalam cairan antinyamuk ...dan pipa horizontal yang terhubung dengan piston. Panjang pipa vertikal yang berada di atas cairan adalah L dengan luas penampang a. Dibutuhkan kecepatan minimum aliran udara v agar cairan anti nyamuk keluar dari pipa vertikal. Setelah pemakaian cairan pipa berkurang sehingga pipa yang berada di atas cairan menjadi 2L, agar semprotan ini tetap berfungsi, maka diperlukan luas penampang pipa yang baru a' sebesar
A. a'= 5a/6
B. a'= a
C. a'= √2a
D. a'= 2a
E. a'= 4a
- Pada keadaan jarak pipa L dari permukaan cairan, tekanan udara dalam tabung adalah
\[\\P_{1}=\frac{\rho v^{2}}{2}+\rho gL\\\\ \frac{F}{A_{1}}=\frac{\rho v^{2}}{2}+\rho gL\]
- Tekanan udara saat jarak pipa 2L dan laju udara v sama seperti kedaan jarak pipa L adalah
\[\\P_{2}=\frac{\rho v^{2}}{2}+\rho g(2L)\\\\ \frac{F}{A_{2}}=\frac{\rho v^{2}}{2}+2\rho gL\]
- Dengan asumsi, dorongan sama yaitu F, perbandingan luas agar cairan tetap keluar dapat diperoleh dengan membandingkan persamaan keadaan L dan 2L
\[\\\frac{A_{2}}{A_{1}}=\frac{\rho v^{2}/2+\rho gL}{\rho v^{2}/2+2\rho gL}\\\\ \frac{A_{2}}{A_{1}}=\frac{1+2\rho gL/v^{2}}{1+4\rho gL/v^{2}}\simeq 1\\A_{2}=A_{1}\\\\ {a}'=a\]
21. Sebuah kawat baja dengan panjang 1m dipanaskan sehingga perubahan panjangnya sama dengan perubahan panjang kawat baja yang diregangkan oleh gaya 1000 N. Jika konstanta elastisitas kawat baja 106N/m dan koefisien muai linier baja 10-5/K, perubahan temperatur yang terjadi pada kawat tersebut adalah
A. 100K
B. 96K
C. 90K
D. 87K
E. 80K
- Perubahan suhu dapat diperoleh dari pertambahan panjang kawat baja.\[\\\Delta L=L_{o}\alpha (\Delta T)\\\\ \frac{F}{k}=L_{o}\alpha (\Delta T)\\\\ \Delta T=\frac{F}{kL_{o}\alpha }\\\\ \Delta T=\frac{10^{3}}{(10^{6})(1)(10^{-5}) }\\\\\Delta T=100K\]
22. Sebuah mesin uap mempunyai efisiensi 80% dari efisiensi ideal yang bekerja di dua reservoir panas yang temperaturnya T1= 327oC dan T2. Daya mesin uap tersebut 3000 watt. Jika besarnya kalor yang dilepaskan setiap detiknya ke reservoir T2adalah 4500 Joule, T2adalah
A. 27oC
B. 77oC
C. 127oC
D. 177oC
E. 227oC
- Temperature rendah dapat dihitung dari persamaan efisiensi mesin.\[\\\eta =\frac{4}{5}.\eta _{ideal}\\\\ \frac{W}{Q_{1}}=\frac{4}{5}\left (1-\frac{T_{2}}{T_{1}} \right )\\\\ \frac{W}{W+Q_{2}}=\frac{4}{5}\left (1-\frac{T_{2}}{T_{1}} \right )\\\\ \left (\frac{3000}{3000+4500} \right )=\frac{4}{5}\left (1-\frac{T_{2}}{600} \right )\\\\ \frac{10}{25}=\frac{4}{5}\left (1-\frac{T_{2}}{600} \right )\\\\ \frac{1}{2}=\frac{T_{2}}{600}\\\\T_{2}=300K=27^{o}C\]
23. Perhatikanlah gambar di bawah ini.
Seutas tali yang tipis disambung dengan tali yang tebal, kemudian diikatkan pada sebuah tembok yang kokoh seperti pada gambar di atas. Jika pada salah satu ujung tali yang tipis diberi gangguan, terjadi gelombang yang merambat ke kanan. Pada saat di A
A. Sebagian gelombang diteruskan dan dipantulkan dgn fase sama gelombang datang
B. Semua gelombang diteruskan menuju B
C. Sebagian gelombang diteruskan dan sebagian dipantulkan
D. Semua gelombang dipantulkan
E. Panjang gelombang yang diteruskan dan dipantulkan sama
Pada saat gelombang melewati titik A, gelombang akan mengalami pemantulan dan pembiasan. Gelombang yang dipantulkan akan memiliki fase yang berlawanan dengan gelombang datang (disebabkan gelombang datang dari medium renggang ke rapat). Sedangkan gelombang yang diteruskan atau ditransmisikan akan memiliki fase yang sama dengan gelombang datang.
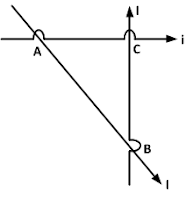
24. Perhatikanlah gambar dibawah ini.
Tiga kawat cukup panjang dibentuk seperti pada gambar. Dua kawat dialiri I dan satu kawat dialiri arus i. Panjang bagian kawat AB adalah L dan AC adalah L/2. Jika belokkan kecil di A, B, dan C diabaikan, besar medan magnet dititik C adalah
A. Nol
B. $\displaystyle \frac{2\mu _{o}I}{\sqrt{3}\pi L}$
C. $\displaystyle \frac{2\mu _{o}i}{\sqrt{3}\pi L}$
D. $\displaystyle \frac{\mu _{o}I}{\sqrt{3}\pi L}$
E. $\displaystyle \frac{\mu _{o}i}{\sqrt{3}\pi L}$
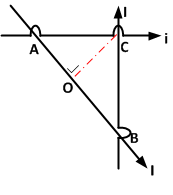
- Medan magnet dititik C hanya dipengaruhi oleh kawat miring (kawat A). Oleh karena itu kita tentukan jarak tegak lurus titik C ke kawat miring (OC). Jarak OC dapat dihitung dengan perbandingan
- Medan magnet dititik C akibat kawat miring adalah \[\\B=\frac{\mu _{o}I_{A}}{2\pi r_{OA}}\\\\ B=\frac{\mu _{o}I}{2\pi (\sqrt{3}L/4)}\\\\ B= \frac{2\mu _{o}I}{\sqrt{3}\pi L}\]
\[\\\frac{OC}{AC}=\frac{BC}{AB}\\\\ OC=\frac{\sqrt{AB^{2}-AC^{2}}}{AB}(AC)\\\\ OC=\frac{\sqrt{L^{2}-(L/2^{2}}}{L}(L/2)\\\\OC=\frac{\sqrt{3}}{4}L\]
25. Sumber arus bolak balik memiliki amplitudo tegangan 200V dan frekuensi sudut 25 Hz mengalir melalui hambatan R = 200 ohm dan kapasitor C = 100µF/πyang disusun seri. Kuat arus yang melalui kapasitor tersebut adalah
A. √2A/4
B. √2A/2
C. √2A
D. 2√2A
E. 5√2A
- Hambatan total (impedansi) rangkaian adalah \[\\X_{C}=\frac{1}{\omega C}\\\\ X_{C}=\frac{1}{(2\pi f)(C)}\\\\ X_{C}=\frac{1}{(2\pi 25)(100\mu /\pi )}\\\\ X_{C}=200\Omega \\\\Z^{2}=R^{2}+(X_{C})^{2}\\\\ Z^{2}=200^{2}+200^{2}\\\\ Z=200\sqrt{2}\Omega\]
- Arus maksimum pada kapasitor akan sama dengan di resistor yaitu \[\\I_{max}=\frac{V_{max}}{Z}\\\\ I_{max}=\frac{200}{200\sqrt{2}}\\\\ I_{max}=\frac{\sqrt{2}}{2}A\]
26. Sebuah benda pada suhu T memancarkan radiasi termal dengan panjang gelombang bervariasi. Radiasi panjang gelombang 580 mikrometer memiliki intensitas maksimum. Jika suhu benda dinaikkan menjadi 2T, panjang gelombang dengan intensitas radiasi maksimum berubah menjadi
A. 72.5 mikrometer
B. 145 mikrometer
C. 290 mikrometer
D. 580 mikrometer
E. 1160 mikrometer
- Panjang gelombang saat suhu mnejadi 2T dapat dihitung dengan rumus hukum Wien dengan cara membandingkan terhadap kondisi pertama. \[\\\lambda T=C\\\\ \lambda _{1}T_{1}=\lambda _{2}T_{2}\\\\ (580)T=\lambda _{2}(2T)\\\\ \lambda _{2}=\frac{580}{2}\mu m\\\\ \lambda _{2}=290\mu m\]
27. Sebuah benda berbentuk kubus dengan volume 1 meterkubik. Jika seorang pengamat berada dalam pesawat yang bergerak dengan kecepatan 0.8c relatif terhadap kubus dalam arah sejajar dengan salah satu rusuk kubus, luas sisi kubus yang teramati adalah
A. 1.4 m2
B. 1.2 m2
C. 1.0 m2
D. 0.8 m2
E. 0.6 m2
- Menurut reativitas khusus Einstein, panjang rusuk kubus yang searah gerakan pesawat akan mengalami pemendekan (kontraksi panjang). \[\\L=L_{o}\sqrt{1-(\frac{v}{c})^{2}}\\\\ L=(1)\sqrt{1-(\frac{0,8c}{c})^{2}}\\\\ L=\sqrt{0.36}=0.6m\]
- Luas satu sisi yang rusuknya sejajar dengan gerak pesawat adalah \[\\A=s_{o}.s\\\\ A=(1)(0.6)m^{2}\\\\ A=0.6m^{2}\]
28. Perhatikanlah gambar di bawah ini.
Tiga muatan q1,q2dan q3disusun membentuk konfigurasi seperti pada gambar. Dititik p besar kuat medan listrik akibat muatan q1sama dengan besar kuat medan listrik akibat muatan q2dan q3.
SEBAB
Di titik p potensial listrik V akibat muatan q1sama dengan tiga kali potensial listrik akibat q2dan q3.
- Perhatikan gambar di bawah ini untuk menentukan resultan kuat medan listrik di p.
- Jarak muatan 2 ke titik p dapat dihitung dengan phitagoras yaitu.\[\\R=2\sqrt{r^{2}-(\frac{r}{2})^{2}}\\\\R=\sqrt{3}r\]
- Karena jarak dan besar muatan muatan 1 dan 3 sama ke titik p, besar kuat medan listrik oleh dua muatan ini sama, dan resultannya dapat dihitung dengan resultan dua vektor mengapit sudut 60.\[\\E_{1}=E_{3}=k\frac{q}{r^{2}}\\\\ E_{31}^{2}=E_{1}^{2}+E_{3}^{2}+2.E_{1}.E_{3}cos60\\\\ E_{31}=\sqrt{3}k\frac{q}{r^{2}}\]
- Besar medan listrik oleh muatan 2 di titik p adalah\[\\E_{2}=k\frac{3\sqrt{3}q}{(\sqrt{3}r)^{2}}\\\\ E_{2}=\sqrt{3}k\frac{q}{r^{2}}\]
- Resultan medan listrik di titik p akibat ketiga muatan adalah NOL
- Potensial dititik p akibat muatan 1 akan sama dengan muatan 3. \[\\V_{1}=V_{3}=k\frac{q}{r}\]
- Potensial akibat muatan 2 dititik p adalah \[\\V_{2}=-3\sqrt{3}k\frac{q}{\sqrt{3}r}\\\\ V_{2}=-3k\frac{q}{r}\]
- Potensial akibat muatan 1 sama dengan dua kali potensial akibat muatan 2 dan 3.
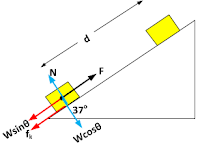
29. Sebuah kotak dengan berat 400N ditarik ke atas oleh gaya F sepanjang bidang miring dengan sudut kemiringan θ (sinθ = 3/5) dan koefisien gesek kinetik 2/5. Kotak bergerak dengan laju tetap dan berpindah sejauh d = 2m. Pernyataan yang benar adalah
1. Usaha oleh gaya F mesin adalah+ 736 Joule
2. Usaha oleh gaya gravitasi -800 Joule
3. Usaha oleh gaya gesek -256 Joule
4. Besar gaya F adalah 112N
Untuk memudahkan membayangkan perhatikanlah gambar di bawah ini.
- Besar gaya gesek kinetik dan gaya F \[\\f_{k}=\mu _{k}Wcos\theta \\\\ f_{k}=\frac{2}{5}(400.\frac{4}{5})N\\\\ f_{k}=128N\\\\ \Sigma F=0\\\\ F-f_{k}-Wsin\theta =0\\\\ F=f_{k}+Wsin\theta \\\\ F=128N+400.\frac{3}{5}N=368N\]
- Usaha oleh gaya F \[\\W_{F}=F.d\\\\ W_{F}=(368N)(2m)\\\\W_{F}=+736 Joule\]
- Usaha oleh gaya gravitasi \[\\W=F.d\\\\ W=-wsin\theta .d\\\\ W=-400.\frac{3}{5}(2)\\\\ W=-480 Joule\]
- Usaha oleh gaya gesek kinetik \[\\W_{f}=f_{k}.d\\\\ W_{f}=-(128)(2)\\\\ W_{f}=-256 Joule\]
30. Pernyataan-pernyataan yang benar mengenai gelombang cahaya di bawah ini adalah
1. Seberkas cahaya yang merambat dari medium udara dan memasuki air tidak mengalami penyerapan sebagian energinya oleh air.
2. Seberkas cahaya dapat mengalami interferensi dalam air.
3. Seberkas cahaya yang merambat dalam medium udara dan memasuki air mengalami perubahan frekuensi.
4. Seberkas cahaya yang merambat dari medium udara dan memasuki air mengalami perubahan panjang gelombang.
- Cahaya ketika memasuki medium yang berbeda akan mengalami penyerapan energi oleh medium yang dilewatinya sehingga intensitasnya akan berkurang
- Seberkas cahaya dalam medium apapun dapat mengalami interferensi asal ada cahaya lain yang koheren.
- Frekuensi gelombang apapun ketika memasuki medium yang berbeda selalu tetap, termasuk cahaya.
- Gelombang akan mengalami perubahan laju dan panjang gelombang ketika memasuki medium dengan kerapatan berbeda.
