Hukum I Kirchoff
Jumlah arus masuk pada sebuah titik percabangan dalam rangkaian listrik, sama dengan jumlah arus yang keluar dari titik tersebut. Secara matematis Hukum I Kirchoff dinyatakan dengan persamaan berikut: \[\Sigma I_{masuk}=\Sigma I_{keluar}\]Contoh ,\[i_{1}+ i_{4}= i_{2}+ i_{3}\]
Hukum II Kirchoff
Pada sebuah rangkaian tertutup, jumlah aljabar GGL (ε) dan jumlah penurunan tegangan (IR) sama dengan nol. Secara matematis Hukum Kirchoff 2 dinyatakan dengan persamaan berikut: \[\Sigma E+\Sigma I.R=0\]Perjanjian tanda- Arus bertanda positif jika searah dengan loop dan bertanda negatif jika berlawanan dengan arah loop.
- GGL bertanda positif jika kutub positifnya lebih dulu dijumpai loop dan sebaliknya GGL negatif jika kutub negatifnya lebih dulu dijumpai loop.
Perhatikan gambar rangkaian di bawah!

Besar kuat arus yang mengalir pada rangkaian tersebut adalah…
Langkah penyelesaian cara Pak Dimpun:

Kita ikuti arah loop mulai dari hambatan 10 Ohm (berlawanan putaran jam)
$\small \\10i-12+5i+5i-20 = 0 \\20i=32 \\i=\frac{32}{20} = 1,6 \: Ampere$ Kuat arus bertanda positip, berarti arah arus listrik yang kita buat benar.
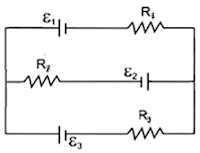
2. Perhatikan gambar rangkaian listrik berikut ini!
Langkah penyelesaian cara Pak Dimpun:
- Gambarkan semua loop dan tentukan kuat arus (simbol dan arahnya)
- Tulislah persamaan setiap loop dengan menggunakan hukum II Kirchoff.
- Tulislah persamaan arus untuk tiap titik percabangan dengan menggunakan hukum I Kirchoff.
- analisa persamaan dengan substitusi atau eliminasi.

Kita ikuti arah loop mulai dari hambatan 10 Ohm (berlawanan putaran jam)
$\small \\10i-12+5i+5i-20 = 0 \\20i=32 \\i=\frac{32}{20} = 1,6 \: Ampere$ Kuat arus bertanda positip, berarti arah arus listrik yang kita buat benar.
2. Perhatikan gambar rangkaian listrik berikut ini!

Jika diketahui ε1 = 16 V, ε2 = 8 V, ε3 = 10 V, R1 = 12 ohm, R2 = 6 ohm, dan R3 = 6 ohm. Tentukan besar kuat arus lisrik I yang melewati R2!
Jawaban Fisika Pak Dimpun:
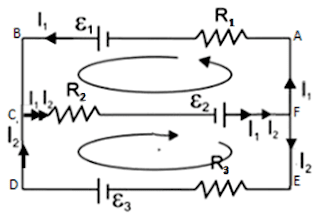
Tulislah persamaan setiap loop dengan menggunakan hukum II Kirchoff.
Jawaban Fisika Pak Dimpun:
Kami melihat, beberapa blog telah membahas soal ini, termasuk blog yang iklannya mungkin menghiasi blog ini, tetapi hasil yang diperoleh belum tepat, dan kami coba membahas dengan sedikit berbeda tetapi dapat kami pertanggungjawabkan ketepatannya.Kita gambarkan semua loop dan tentukan kuat arus (simbol dan arahnya)

Analisa loop ABCFA, ikuti arah loop, kita mulai dari A.
$\small \\i_1R_1-\varepsilon _1 +(i_1+i_2)R_2-\varepsilon _2=0 \\i_1(12)-16+(i_1+i_2)6-8=0\\18i+6i_2=24......(1)$
Analisa loop DCFED, ikuti arah loop, kita mulai dari E.
$\small \\i_2R_3-\varepsilon _3+(i_1+i_2)R_2-\varepsilon _2=0\\i_2(6)-10+(i_1+i_2)6-8=0\\6i_1+12i_2=18\\3i_1+6I_2=9.....(2)$
eliminasi kedua persamaan
$\begin{align*} &18i+6i_2=24....(1)\\&3i_1+6i_2=9.....(2)-\\\hline &15i_1=15\\&i_1=1A\end{align*}$
$\begin{align*}3i_1+6i_2&=9\\3(1)+6i_2&=9\\6I_2&=6\\i_2&=1\: A\end{align*}$
Arus pada R2 =i1+i2=1+1=2A
$\small \\i_1R_1-\varepsilon _1 +(i_1+i_2)R_2-\varepsilon _2=0 \\i_1(12)-16+(i_1+i_2)6-8=0\\18i+6i_2=24......(1)$
Analisa loop DCFED, ikuti arah loop, kita mulai dari E.
$\small \\i_2R_3-\varepsilon _3+(i_1+i_2)R_2-\varepsilon _2=0\\i_2(6)-10+(i_1+i_2)6-8=0\\6i_1+12i_2=18\\3i_1+6I_2=9.....(2)$
eliminasi kedua persamaan
$\begin{align*} &18i+6i_2=24....(1)\\&3i_1+6i_2=9.....(2)-\\\hline &15i_1=15\\&i_1=1A\end{align*}$
$\begin{align*}3i_1+6i_2&=9\\3(1)+6i_2&=9\\6I_2&=6\\i_2&=1\: A\end{align*}$
Arus pada R2 =i1+i2=1+1=2A








