SEBUAH PERAHU MENYEBERANGI SUNGAI YANG LEBARNYA 180 M

Soal Dan Penyelesaian Fisika SMA:  Perpaduan GLB dan GLB - Suatu partikel dapat melakukan gerak satu dimensi (Gerak Lurus), baik itu Gerak Lurus Beraturan (GLB) maupun Gerak Lurus Berubah Beraturan (GLBB) juga dapat melakukan gerak dua dimensi, seperti: Gerak suatu perahu ketika menyeberangi sungai, Gerak Parabola, gerak dilempar mendatar, dan lain-lain.

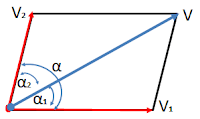
Perpaduan GLB dan GLB, menghasilkan GLB

Perhatikan gerak, yang sudah digambarkan dalam bentuk vektor:

$$\\V=\sqrt{V_1{^{2}}+V_2{^{2}}+2V_1V_2\cos \alpha }\\\\\frac{V_{1}}{\sin \alpha _{2}}=\frac{V_{2}}{\sin \alpha _{1}}=\frac{V}{\sin \alpha }$$ Gerak resultannya $v$ adalah juga merupakan sebuah gerak lurus beraturan. Kalau arah resultannya $v_{1}$ dan $v_{2}$ berimpit, maka gerak resultannya adalah tetap sebuah gerak lurus beraturan juga.

Contoh paduan gerak GLB dengan GLB adalah sebuah perahu menyeberangi sungai:

Andaikan kecepatan aliran sungai adalah $v_{a}$ , kecepatan perahu $v_{p}$ , lebar sungai $L_{s}$ dan waktu tempuh t, maka:

• Waktu yang dibutuhkan perahu untuk menyeberang $t=\frac{L_{s}}{v_{p}}$
• Kecepatan resultan $v=\sqrt{v_{p}^{2}+v_{a}^{2}}$
• Panjang lintasan perahu sampai di seberang $x=\frac{L_{s}}{v_{p}}.\sqrt{v_{p}^{2}+v_{a}^{2}}$

Contoh soal:

---

Sebuah perahu menyeberangi sungai yang lebarnya 180 m dan kecepatan airnya 4 m/s. Bila perahu diarahkan menyilang tegak lurus dengan kecepatan 3 m/s, tentukan panjang lintasan yang ditempuh perahu hingga sampai ke seberang sungai! (Sumber Soal : UMPTN)

Jawaban Fisika dari Pak Dimpun: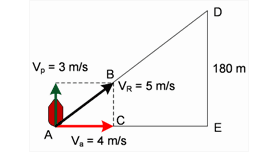

$$\\x=\frac{L_{s}}{v_{p}}.\sqrt{v_{p}^{2}+v_{a}^{2}}\\\\ x=\frac{180}{3}.\sqrt{3^{2}+4^{2}}\\\\x=300m$$