Titik berat adalah titik kesetimbangan suatu benda ataupun suatu bangun baik itu panjang, luas, atau volume yang dapat diartikan sebagai titik yang menjadi penyeimbang dari suatu bangun.
Langkah mudah menghitung koordinat titik berat benda ala Pak Dimpun:
- Bagi benda, menjadi beberapa bagian sederhana.
- Hitung (tergantung bentuk benda)
- panjang (garis - satu dimensi) :$L_1, L_2, dst$
- luas (luasan - dua dimensi) :$A_1, A_2, dst$
- volume (tiga dimensi) :$V_1, V_2, dst$
- massa, berat, dll ( benda titik) :$m_1, m_2, dst$ masing-masing bagian;
- Tentukan koordinat titik berat masing-masing bagian ( X, Y: ) \begin{align*} &(X_1,Y_1)\\&(X_2,Y_2)\\&dst...\end{align*}
- Hitung Xo dan Yo : Misalkan benda berbentuk garis, maka yang kita hitung adalah panjang, persamaan menjadi: \begin{align*} X_o&=\frac {L_1X_1+L_2X_2+L_3X_3+...}{L_1+L_2+L_3+...} \\Y_o&=\frac {L_1Y_1+L_2Y_2+L_3Y_3+...}{L_1+L_2+L_3+...}\end{align*}
- Tuliskan koordinat titik berat benda;\begin{align*} Z_o&=(X_o;Y_o)\end{align*}
Benda berbentuk panjang (satu dimensi)
Contoh 1. Tentukan koordinat titik berat dari bangun berikut!
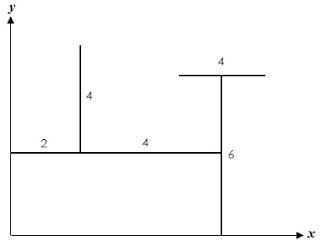
Penyelesaian Fisika:
Kita ikuti Langkah mudah ala Pak Dimpun:
- Kita bagi benda, dalam hal ini kita bagi menjadi 4 bagian

- Kita hitung panjang masing-masing bagian: \begin{align*} L_1&=4\\L_2&=6\\L_3&=6\\L_4&=4\end{align*}
- Kita tentukan koordinat titik berat masing-masing bagian, untuk benda homogen titik berat persis di tengah. \begin{align*} (X_1;Y_1)&=(2;5)\\(X_2;Y_2)&=(3;3)\\(X_3;Y_3)&=(6;3)\\(X_4;Y_4)&=(6;6)\end{align*}
- Kita hitung Xo dan Yo: \begin{align*} X_o&=\frac {L_1X_1+L_2X_2+L_3X_3+L_4X_4}{L_1+L_2+L_3+L_4} \\X_o&=\frac {4(2)+6(3)+6(6)+4(6)}{4+6+6+4}\\X_o&=\frac {86}{20}=4,3\\\\Y_o&=\frac {L_1Y_1+L_2Y_2+L_3Y_3+L_4Y_4}{L_1+L_2+L_3+L_4} \\Y_o&=\frac {5(4)+3(6)+4(6)+4(6)}{4+6+6+4}\\Y_o&=\frac {80}{20}=4\end{align*}
- Kita tuliskan koordinat titik berat benda;\begin{align*} Z_o&=(4,3;4)\end{align*}
Benda berbentuk Luasan (dua Dimensi)
Contoh 2. Tentukan letak koordinat titik berat bidang yang diarsir pada gambar berikut!

Penyelesaian Fisika:
Kita ikuti Langkah mudah ala Pak Dimpun:
- Kita bagi benda, dalam hal ini kita bagi menjadi 2 bagian, satu persegipanjang utuh dan satu segitiga dibuang atau dikurangi dari persegipanjang utuh tersebut (tidak diarsir)
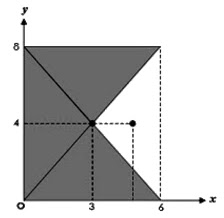
- Kita hitung Luas masing-masing bagian: \begin{align*} A_1&=8x6=48\\A_2&=-0,5(8x3)=-12\end{align*}tanda negatip karena luas ini dikurangi dari luas bagian pertama.
- Kita tentukan koordinat titik berat masing-masing bagian, untuk benda homogen titik berat persis di tengah. \begin{align*} X_1&=\frac{1}{2}(6)=3\\Y_1&=\frac{1}{2}(8)=4\\X_2&=6-\frac{1}{3}(h)\\&=6-\frac{1}{3}(3)=5\\Y_2&=\frac{1}{2}(8)=4\end{align*}
- Kita hitung Xo dan Yo: \begin{align*} X_o&=\frac {A_1X_1+A_2X_2}{A_1+A_2} \\X_o&=\frac {48(3)+(-12)(5)}{48-12}\\X_o&=\frac {84}{36}=2,3\\\\Y_o&=\frac {A_1Y_1+A_2Y_2}{A_1+A_2} \\Y_o&=\frac {48(4)+(-12)(4)}{48-12} \\Y_o&=\frac {144}{36}=4\end{align*}
- Kita tuliskan koordinat titik berat benda;\begin{align*} Z_o&=(2,3;4)\end{align*}
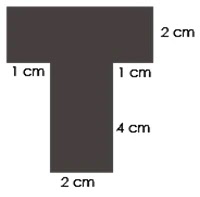
Penyelesaian Fisika:
Kita ikuti Langkah mudah ala Pak Dimpun:
- Kita bagi benda, dalam hal ini kita bagi menjadi 2 bagian, satu persegi panjang bawah yang vertikal dan satu persegi panjang atas yang horizontal.
- Kita hitung Luas masing-masing bagian: \begin{align*} A_1&=2x4=8\\A_2&=4x2=8\end{align*}
- Kita tentukan koordinat titik berat masing-masing bagian, untuk benda homogen titik berat persis di tengah. \begin{align*} X_1&=1+\frac{1}{2}(2)=2\\Y_1&=\frac{1}{2}(4)=2\\X_2&=\frac{1}{2}(4)=2\\Y_2&=4+\frac{1}{2}(2)=5\end{align*}
- Kita hitung Xo dan Yo: \begin{align*} X_o&=\frac {A_1X_1+A_2X_2}{A_1+A_2} \\X_o&=\frac {8(2)+8(2)}{8+8}=2\\\\Y_o&=\frac {A_1Y_1+A_2Y_2}{A_1+A_2} \\Y_o&=\frac {8(2)+8(5)}{8+8}=3,5 \end{align*}
- Kita tuliskan koordinat titik berat benda;\begin{align*} Z_o&=(2;3,5)\end{align*}








