Kita lanjut bahas Soal Titik Berat selanjutnya...
SOAL DAN PENYELESAIAN TITIK BERAT DAN PUSAT MASSA
Soal 1. Sistem tiga partikel yang saling dihubungkan dengan bidang enteng tidak bermasa terletak pada satu sistem koordinat menyerupai pada gambar di bawah ini. Tentukanlah sentra massa sistem.
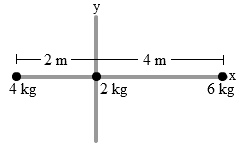
Penyelesaian Fisika Titik Berat:
\[X_o=\frac{m_1.X_1+m_2.X_2+m_3.X_3}{m_1+m_2+m_3}\\X_o=\frac{4.(-2)+2(0)+6(4)}{4+2+6}\\X_o=\frac{16}{12}=\frac{4}{3}\]
Soal 2. Koordinat titik berat bidang pada gambar di bawah ini adalah...?
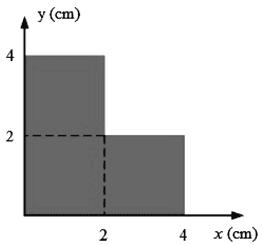
Penyelesaian Fisika Titik Berat:
Mari kita ikuti langkah ala Pak Dimpun:
a. Kita bagi benda, menjadi DUA.
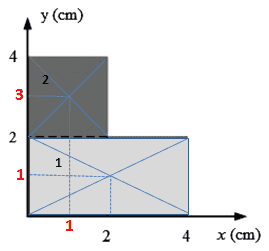
b. Kita hitung luas masing-masing;\[A_1=4\times 2=8\\A_2=2\times 2=4\]c. Kita cari koordinat titik berat masing-masing;\[X_1=2;Y_1=1\\X_2=1;Y_2=3\]d. Hitung Xo dan Yo\[X_o=\frac{A_1.X_1+A_2.X_2}{A_1+A_2}\\X_o=\frac{8\times 2+4\times 1}{8+4}\\X_o=\frac{20}{12}=\frac{5}{3}=2,67\]\[Y_o=\frac{A_1.Y_1+A_2.Y_2}{A_1+A_2}\\Y_o=\frac{8\times 1+4\times 3}{8+4}\\Y_o=\frac{20}{12}=\frac{5}{3}=2,67\]e. Tuliskan titik berat;\[Z=(1,67;1,67)\]
Soal 3. Terdapat dua bidang disatukan menjadi seperti gambar di bawah ini. Koordinat titik beratnya adalah ?
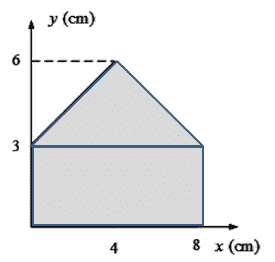
Soal 3. Terdapat dua bidang disatukan menjadi seperti gambar di bawah ini. Koordinat titik beratnya adalah ?

Penyelesaian Fisika Titik Berat:
b. Kita hitung luas masing-masing;\[A_1=8\times 3=24\\A_2=\frac{1}{2}.8\times 3=12\]c. Kita cari koordinat titik berat masing-masing;\[X_1=4;Y_1=1,5\\X_2=4;Y_2=3+\frac{1}{3}(3)=4\]d. Hitung Xo dan Yo
Karena X kedua benda sama, maka Xo=4;\[Y_o=\frac{A_1.Y_1+A_2.Y_2}{A_1+A_2}\\Y_o=\frac{24\times 1,5+12\times 4}{24+12}\\Y_o=\frac{84}{36}=2,33\]e. Tuliskan titik berat;\[Z=(4;2,33)\]
Soal 4. Jika sebuah pelat dibentuk menjadi seperti terlihat di bawah ini, tentukanlah titik berat pelat tersebut.

a. Kita bagi benda, menjadi TIGA; Anggap setengah lingkaran besar (berjari-jari R) adalah utuh lalu dikurangi dua buah setengah lingkaran kecil (berjari-jari 0,5R).
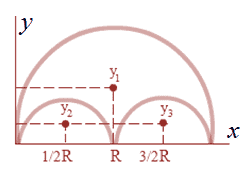
b. Kita hitung luas masing-masing;
\[A_1=\frac{1}{2}\pi R^{2}\\A_2=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\\A_3=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\]c. Kita cari koordinat titik berat masing-masing;
\[X_1=R;\, Y_1=\frac{4R}{3\pi}\\X_2=\frac{1}{2} R;Y_2=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\\X_3=\frac{3}{2} R; Y_3=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\]d. Hitung Xo dan Yo
Karena X kedua benda sama, maka Xo=4;\[X_o=\frac{A_1.X_1+A_2.X_2+A_3.X_3}{A_1+A_2+A_3} \\X_o=\frac{\frac{1}{2}\pi R^2(R) -\frac{1}{8}\pi R^2(\frac{R}{2})-\frac{1}{8}\pi R^2(\frac{3R}{2 })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\X_o=\frac{4(R) -(\frac{R}{2 })-(\frac{3R}{2 })}{2}=\frac{4R}{4}\\X_o=R\]\[Y_o=\frac{A_1.Y_1+A_2.Y_2+A_3.Y_3}{A_1+A_2+A_3} \\Y_o=\frac{\frac{1}{2}\pi R^2(\frac{4R}{3\pi }) -\frac{1}{8}\pi R^2(\frac{2R}{3\pi })-\frac{1}{8}\pi R^2(\frac{2R}{3\pi })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\Y_o=\frac{4(\frac{4R}{3\pi }) -(\frac{2R}{3\pi })-(\frac{2R}{3\pi })}{2}=\frac{12R}{6\pi}\\Y_o=\frac{2R}{\pi}\]e. Tuliskan titik berat;\[Z=(R,\frac{2R}{\pi})\]

Karena X kedua benda sama, maka Xo=4;\[Y_o=\frac{A_1.Y_1+A_2.Y_2}{A_1+A_2}\\Y_o=\frac{24\times 1,5+12\times 4}{24+12}\\Y_o=\frac{84}{36}=2,33\]e. Tuliskan titik berat;\[Z=(4;2,33)\]
Soal 4. Jika sebuah pelat dibentuk menjadi seperti terlihat di bawah ini, tentukanlah titik berat pelat tersebut.

Penyelesaian Fisika Titik Berat:
Mari kita ikuti langkah ala Pak Dimpun:a. Kita bagi benda, menjadi TIGA; Anggap setengah lingkaran besar (berjari-jari R) adalah utuh lalu dikurangi dua buah setengah lingkaran kecil (berjari-jari 0,5R).

b. Kita hitung luas masing-masing;
\[A_1=\frac{1}{2}\pi R^{2}\\A_2=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\\A_3=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\]c. Kita cari koordinat titik berat masing-masing;
\[X_1=R;\, Y_1=\frac{4R}{3\pi}\\X_2=\frac{1}{2} R;Y_2=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\\X_3=\frac{3}{2} R; Y_3=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\]d. Hitung Xo dan Yo
Karena X kedua benda sama, maka Xo=4;\[X_o=\frac{A_1.X_1+A_2.X_2+A_3.X_3}{A_1+A_2+A_3} \\X_o=\frac{\frac{1}{2}\pi R^2(R) -\frac{1}{8}\pi R^2(\frac{R}{2})-\frac{1}{8}\pi R^2(\frac{3R}{2 })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\X_o=\frac{4(R) -(\frac{R}{2 })-(\frac{3R}{2 })}{2}=\frac{4R}{4}\\X_o=R\]\[Y_o=\frac{A_1.Y_1+A_2.Y_2+A_3.Y_3}{A_1+A_2+A_3} \\Y_o=\frac{\frac{1}{2}\pi R^2(\frac{4R}{3\pi }) -\frac{1}{8}\pi R^2(\frac{2R}{3\pi })-\frac{1}{8}\pi R^2(\frac{2R}{3\pi })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\Y_o=\frac{4(\frac{4R}{3\pi }) -(\frac{2R}{3\pi })-(\frac{2R}{3\pi })}{2}=\frac{12R}{6\pi}\\Y_o=\frac{2R}{\pi}\]e. Tuliskan titik berat;\[Z=(R,\frac{2R}{\pi})\]
Soal 5. Sebuah plat bujursangkar diberi lubang berupa lingkaran berdiameter 1cm. Letak koordinat titik berat bidang adalah ?

Penyelesaian Fisika Titik Berat:
Mari kita ikuti langkah ala Pak Dimpun:
a. Kita bagi benda, menjadi DUA; Anggap bujursangkar utuh lalu dikurangi lingkaran (berjari-jari 0,5cm)
b. Kita hitung luas masing-masing;\[A_1=4\times 4=16\\A_2=-\pi R^2=\pi (1)^2=-\pi\]c. Kita cari koordinat titik berat masing-masing;\[X_1=2;Y_1=2\\X_2=3;Y_2=2\]d. Hitung Xo dan Yo
Karena Y kedua benda sama, maka Yo=2;\[X_o=\frac{A_1.X_1+A_2.X_2}{A_1+A_2}\\X_o=\frac{(16\times 2)-(\pi \times 3)}{16-\pi}\\X_o=\frac{(16\times 2)-(3,14 \times 3)}{16-3,14}\\X_o=\frac{22,58}{12,58}=1,76\]e. Tuliskan titik berat;\[Z=(1,76;2)\] Lanjut soal berikutnya....
Mari kita ikuti langkah ala Pak Dimpun:
a. Kita bagi benda, menjadi DUA; Anggap bujursangkar utuh lalu dikurangi lingkaran (berjari-jari 0,5cm)
b. Kita hitung luas masing-masing;\[A_1=4\times 4=16\\A_2=-\pi R^2=\pi (1)^2=-\pi\]c. Kita cari koordinat titik berat masing-masing;\[X_1=2;Y_1=2\\X_2=3;Y_2=2\]d. Hitung Xo dan Yo
Karena Y kedua benda sama, maka Yo=2;\[X_o=\frac{A_1.X_1+A_2.X_2}{A_1+A_2}\\X_o=\frac{(16\times 2)-(\pi \times 3)}{16-\pi}\\X_o=\frac{(16\times 2)-(3,14 \times 3)}{16-3,14}\\X_o=\frac{22,58}{12,58}=1,76\]e. Tuliskan titik berat;\[Z=(1,76;2)\] Lanjut soal berikutnya....