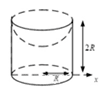
Soal 1. Tentukan tinggi pusat massa sebuah silinder pejal setinggi 2h yang terpancung dengan ukuran setengah bola berjari-jari R pada bagian atas seperti pada gambar!
A. $\frac{33}{24}$ R
B. $\frac{33}{16}$ R
C. $\frac{11}{16}$R
D. $\frac{19}{16}$ R
E. $\frac{19}{24}$ R
Jawaban Fisika dari Pak Dimpun
Kita bagi benda menjadi dua bagian, yaitu:
Bagian Pertama, slinder pejal utuh.\begin{align*}V_1=\pi R^{2}.2R=2\pi R^3 \\y_1=\frac{1}{2}t=\frac{1}{2}.2R=R\end{align*} Bagian kedua, dikurangi setengah bola terbalik. \begin{align*}V_2&=-\frac{1}{2}.\frac{4}{3}\pi R^{3}=-\frac{2}{3}\pi R^3 \\y_2&=2R-\frac{3}{8}R=\frac{13}{8}R\end{align*} Tinggi titik berat susunan bangun: \begin{align*} y_{o}&=\frac{\Sigma V.y}{\Sigma V}=\frac{V_{1}.y_{1}+V_{2}.y_{2}}{ A_{1}+A_{2}}\\\\y_{o}&=\frac{2\pi R^{3}.(R)-\frac{2}{3}\pi R^{3}.(\frac{13}{8}R)}{2\pi R^{3}-\frac{2}{3}\pi R^{3}}\\y_{o}&=\frac{R-\frac{3}{24}R}{1-\frac{2}{3}}\\y_{o}&=\frac{11}{16}R\end{align*}
Soal 2. SPMB 2002 Regional I Sebuah roda akan dinaikan pada anak tangga seperti pada gambar.
Bila jari-jari = R, berat roda = W, tinggi anak tangga = h, maka gaya F minimum yang dibutuhkan agar roda tersebut dapat naik adalah....
A. W(R-h)
B. $\frac{W(2Rh-h^{2})^{\frac{1}{2}}}{R-h}$
C. $W(2Rh-h^{2})^{\frac{1}{2}}$
D.$\frac{W(R-h)}{R}$
E. $\frac{Wh}{R-h}$
Jawaban Fisika dari Pak Dimpun
Ini gaya pada rodanya:
Kita hitung jarak x:
B. $\frac{33}{16}$ R
C. $\frac{11}{16}$R
D. $\frac{19}{16}$ R
E. $\frac{19}{24}$ R
Jawaban Fisika dari Pak Dimpun
Kita bagi benda menjadi dua bagian, yaitu:
Bagian Pertama, slinder pejal utuh.\begin{align*}V_1=\pi R^{2}.2R=2\pi R^3 \\y_1=\frac{1}{2}t=\frac{1}{2}.2R=R\end{align*} Bagian kedua, dikurangi setengah bola terbalik. \begin{align*}V_2&=-\frac{1}{2}.\frac{4}{3}\pi R^{3}=-\frac{2}{3}\pi R^3 \\y_2&=2R-\frac{3}{8}R=\frac{13}{8}R\end{align*} Tinggi titik berat susunan bangun: \begin{align*} y_{o}&=\frac{\Sigma V.y}{\Sigma V}=\frac{V_{1}.y_{1}+V_{2}.y_{2}}{ A_{1}+A_{2}}\\\\y_{o}&=\frac{2\pi R^{3}.(R)-\frac{2}{3}\pi R^{3}.(\frac{13}{8}R)}{2\pi R^{3}-\frac{2}{3}\pi R^{3}}\\y_{o}&=\frac{R-\frac{3}{24}R}{1-\frac{2}{3}}\\y_{o}&=\frac{11}{16}R\end{align*}
Soal 2. SPMB 2002 Regional I Sebuah roda akan dinaikan pada anak tangga seperti pada gambar.
A. W(R-h)
B. $\frac{W(2Rh-h^{2})^{\frac{1}{2}}}{R-h}$
C. $W(2Rh-h^{2})^{\frac{1}{2}}$
D.$\frac{W(R-h)}{R}$
E. $\frac{Wh}{R-h}$
Jawaban Fisika dari Pak Dimpun
Ini gaya pada rodanya:
$x=\sqrt{R^{2}-(R-h)^{2}}\\x=\sqrt{2Rh-h^{2}}$ Ambil jumlah momen gaya di A sama dengan NOL
\begin{align*} \Sigma \tau _{A}&=0\\W(x)&=F(R-h)\\W(\sqrt{2Rh-h^{2}})&=F(R-h)\\F&=\frac{W\left (2Rh-h^{2} \right )^{\frac{1}{2}}}{(R-h)}\end{align*}
C. $\frac{25}{12}$ a
D. 2,3 a
E. $\frac{23}{12}$ a
Jawaban Fisika dari Pak Dimpun
Kita bagi benda menjadi tiga bagian, seperti gambar berikut:
Bidang I:\begin{align*} A_1&=p.l=a.(4a)=4a^2 \\y_1&=\frac{1}{2}a\end{align*}Bidang II:\begin{align*} A_1&=p.l=a.(2a)=2a^2 \\y_1&=a+\frac{1}{2}a=\frac{3}{2}a\end{align*}Bidang III:\begin{align*} A_3&=\frac{1}{2}alas.tinggi\\A_3&=\frac{1}{2}4a.3a=6a^2 \\y_3&=2a+\frac{1}{3}.3a=3a\end{align*}
Tinggi titik berat susunan bidang:\begin{align*} y_{o}&=\frac{\Sigma A.y}{\Sigma A}\\\\ y_{o}&=\frac{A_{1}.y_{1}+A_{2}.y_{2}+A_{3}.y_{3}}{ A_{1}+A_{2}+A_{3}}\\\\y_{o}&=\frac{4a^{2}.(\frac{1}{2}a)+2a^{2}.(\frac{3}{2}a)+6a^{2}.(2a)}{4a^{2}+2a^{2}+6a^{2}}\\\\y_{o}&=\frac{23}{12}a\end{align*}Lanjut soal sebelumnya...
\begin{align*} \Sigma \tau _{A}&=0\\W(x)&=F(R-h)\\W(\sqrt{2Rh-h^{2}})&=F(R-h)\\F&=\frac{W\left (2Rh-h^{2} \right )^{\frac{1}{2}}}{(R-h)}\end{align*}
Soal 3. Tentukan tinggi pusat koordinat massa susunan bidang luas seperti terlihat pada gambar
A. $\frac{21}{7}$ a
B. 2,5 aC. $\frac{25}{12}$ a
D. 2,3 a
E. $\frac{23}{12}$ a
Jawaban Fisika dari Pak Dimpun
Kita bagi benda menjadi tiga bagian, seperti gambar berikut:
