Beberapa penyebab ketidakpastian dalam pengukuran, yaitu:
Ada dua jenis ketidakpastian pengukuran, yaitu pengukuran tunggal dan pengukuran berulang.
1. Ketidakpastian pengukuran tunggal
Pengukuran tunggal merupakan pengukuran yang hanya dilakukan satu kali. Nilai ketidakpastian (Δx) pada pengukuran tunggal diperhitungkan dari skala terkecil (nst) alat ukur yang dipakai. Nilai dari ketidakpastian pada pengukuran tunggal adalah setengah dari skala terkecil pada alat ukur
Misalkan seorang pengamat mengukur panjang pensil menggunakan mistar diperoleh nilai benar sebesar 10 cm. Skala terkecil dari mistar adalah 1 mm atau 0,1 cm maka $\small \Delta x=\frac{1}{2}\times\mbox{nst}=\frac{1}{2}\times0,1=0,05$ . Hasil pengukuran tunggal ini dituliskan sebagai $\small L=10\pm0,05$ cm.
2. Ketidakpastain pengukuran berulang
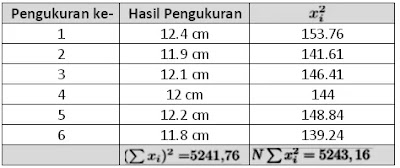
Pengukuran berulang adalah pengukuran yang dilakukan beberapa kali atau berulang-ulang. Dalam pengukuran berulang, pengganti nilai benar adalah nilai rata-rata dari hasil pengukuran.
Secara matematis dapat ditulis sebagai berikut.
$\small \begin{align*} \bar{x}&=\frac{x_{1}+x_{2}+x_{3}+...+x_{n}}{N}\\&=\frac{\sum x_{i}}{N}\\\Delta x&=\frac{1}{N}\sqrt{\frac{N\sum x_{i}^{2}-(\sum x_{i})^{2}}{N-1}}\end{align*}$
Keterangan:
$\small \bar{x}$ : hasil pengukuran yang mendekati nilai benar
$\small \Delta x$ : ketidakpastian pengukuran
$\small N$ : banyaknya pengukuran yang dilakukan.
Pada pengukuran berulang dikenal istilah ketidak pastian relatif, yaitu perbandingan ketidakpastian pengukuran berulang dengan nilai rata-rata pengukuran.
ketidakpastian relatif $=\frac{\Delta x}{\bar{x}}\times100%$
- Kesalahan umum, akibat keterbatasan pengamat saat melakukan pengukuran. Contoh: salah membaca hasil pengukuran,
- Kesalahan sistem, akibat kesalahan instrumen pengukuran. Contoh: alat rusak,
- Kesalahan acak, akibat fluktuasi pada saat pengukuran. Contoh: noise pada pengukuran seismik.
Ada dua jenis ketidakpastian pengukuran, yaitu pengukuran tunggal dan pengukuran berulang.
1. Ketidakpastian pengukuran tunggal
Misalkan seorang pengamat mengukur panjang pensil menggunakan mistar diperoleh nilai benar sebesar 10 cm. Skala terkecil dari mistar adalah 1 mm atau 0,1 cm maka $\small \Delta x=\frac{1}{2}\times\mbox{nst}=\frac{1}{2}\times0,1=0,05$ . Hasil pengukuran tunggal ini dituliskan sebagai $\small L=10\pm0,05$ cm.
2. Ketidakpastain pengukuran berulang
Pengukuran berulang adalah pengukuran yang dilakukan beberapa kali atau berulang-ulang. Dalam pengukuran berulang, pengganti nilai benar adalah nilai rata-rata dari hasil pengukuran.
Secara matematis dapat ditulis sebagai berikut.
$\small \begin{align*} \bar{x}&=\frac{x_{1}+x_{2}+x_{3}+...+x_{n}}{N}\\&=\frac{\sum x_{i}}{N}\\\Delta x&=\frac{1}{N}\sqrt{\frac{N\sum x_{i}^{2}-(\sum x_{i})^{2}}{N-1}}\end{align*}$
Keterangan:
$\small \bar{x}$ : hasil pengukuran yang mendekati nilai benar
$\small \Delta x$ : ketidakpastian pengukuran
$\small N$ : banyaknya pengukuran yang dilakukan.
Pada pengukuran berulang dikenal istilah ketidak pastian relatif, yaitu perbandingan ketidakpastian pengukuran berulang dengan nilai rata-rata pengukuran.
ketidakpastian relatif $=\frac{\Delta x}{\bar{x}}\times100%$
Nilai ketidakpastian relatif menentukan banyaknya angka yang boleh disertakan pada laporan hasil pengukuran. Aturan banyaknya angka yang dapat dilaporkan dalam pengukuran berulang adalah sebagai berikut.
Ada empat aturan dasar dalam perhitungan yang melibatkan teori ketidakpastian fisika.
1. Aturan Penjumlahan dan Pengurangan
Jika dua besaran dijumlahkan atau dikurangkan aturannya adalah tambahkan ketidakpastian mutlaknya. Secara matematis dituliskan:
$\small \begin{align*} \left(x\pm\Delta x\right)+\left(y\pm\Delta y\right)=(x+y)\pm(\Delta x+\Delta y)\\\left(x\pm\Delta x\right)-\left(y\pm\Delta y\right)=(x-y)\pm(\Delta x+\Delta y) \end{align*}$
Contoh:
Penjumlahan:
$\small (5,0\pm0,5)\mbox{ m}+(8,5\pm0,1)\mbox{ m}=\left(13,5\pm0,6\right)\mbox{m}$
Pengurangan:
$\small (16,0\pm0,5)\mbox{ m}-(6,5\pm0,1)\mbox{ m}=\left(10,5\pm0,6\right)\mbox{m}$
2. Aturan Perkalian dan Pembagian
Jika dua besaran terlibat operasi perkalian dan pembagian maka tambahkan ketidakpastian relatifnya.
Contoh:
Ukuran sebuah persegi panjang adalah $\small 5\pm0,1$ cm dan $\small 10\pm0,5$ cm, maka ketidak pastian luasnya adalah...
Penyelesaian Fisika:
Luas persegi panjang $\small L=p\times l$ dengan $\small p=x\pm\Delta x$ dan $\small l=y\pm\Delta y$. Ketidakpastian luas persegi panjang dituliskan sebagai:
$\frac{\Delta L}{L}=\frac{\Delta x}{x}+\frac{\Delta y}{y}$
sehingga:
$\small \begin{align*} \frac{\Delta L}{L} & =\left(\frac{\Delta x}{x}+\frac{\Delta y}{y}\right)\\ \frac{\Delta L}{50} & =\left(\frac{0,1}{5}+\frac{0,5}{10}\right)\\\Delta L & =0,7\times 50\\ \Delta L & =3,5\end{align*}$
3. Aturan Pangkat
Jika $P=x^{n}$ dengan $x=x_{o}\pm\Delta x$, maka $\frac{\Delta P}{P}=n\frac{\Delta x}{x}$.
4. Aturan Perkalian dengan Konstanta
Jika nilai hasil pengukuran yang mengandung ketidakpastian relatif dikalikan dengan sebuah konstanta maka ketidakpastian relatif tidak ikut dikalikan. Tetapi jika hasil pengukurannya mengandung ketidakpastian mutlak maka nilai ketidakpastian harus ikut dikalikan dengan konstanta.
Jika $x=x_{o}\pm\frac{\Delta x}{x_{o}}$,
- relatif 10 % berhak atas dua angka
- relatif 1%berhak atas tiga angka
- relatif 0,1% berhak atas empat angka
Ada empat aturan dasar dalam perhitungan yang melibatkan teori ketidakpastian fisika.
1. Aturan Penjumlahan dan Pengurangan
Jika dua besaran dijumlahkan atau dikurangkan aturannya adalah tambahkan ketidakpastian mutlaknya. Secara matematis dituliskan:
$\small \begin{align*} \left(x\pm\Delta x\right)+\left(y\pm\Delta y\right)=(x+y)\pm(\Delta x+\Delta y)\\\left(x\pm\Delta x\right)-\left(y\pm\Delta y\right)=(x-y)\pm(\Delta x+\Delta y) \end{align*}$
Contoh:
Penjumlahan:
$\small (5,0\pm0,5)\mbox{ m}+(8,5\pm0,1)\mbox{ m}=\left(13,5\pm0,6\right)\mbox{m}$
Pengurangan:
$\small (16,0\pm0,5)\mbox{ m}-(6,5\pm0,1)\mbox{ m}=\left(10,5\pm0,6\right)\mbox{m}$
2. Aturan Perkalian dan Pembagian
Jika dua besaran terlibat operasi perkalian dan pembagian maka tambahkan ketidakpastian relatifnya.
Contoh:
Ukuran sebuah persegi panjang adalah $\small 5\pm0,1$ cm dan $\small 10\pm0,5$ cm, maka ketidak pastian luasnya adalah...
Penyelesaian Fisika:
Luas persegi panjang $\small L=p\times l$ dengan $\small p=x\pm\Delta x$ dan $\small l=y\pm\Delta y$. Ketidakpastian luas persegi panjang dituliskan sebagai:
$\frac{\Delta L}{L}=\frac{\Delta x}{x}+\frac{\Delta y}{y}$
sehingga:
$\small \begin{align*} \frac{\Delta L}{L} & =\left(\frac{\Delta x}{x}+\frac{\Delta y}{y}\right)\\ \frac{\Delta L}{50} & =\left(\frac{0,1}{5}+\frac{0,5}{10}\right)\\\Delta L & =0,7\times 50\\ \Delta L & =3,5\end{align*}$
3. Aturan Pangkat
Jika $P=x^{n}$ dengan $x=x_{o}\pm\Delta x$, maka $\frac{\Delta P}{P}=n\frac{\Delta x}{x}$.
4. Aturan Perkalian dengan Konstanta
Jika nilai hasil pengukuran yang mengandung ketidakpastian relatif dikalikan dengan sebuah konstanta maka ketidakpastian relatif tidak ikut dikalikan. Tetapi jika hasil pengukurannya mengandung ketidakpastian mutlak maka nilai ketidakpastian harus ikut dikalikan dengan konstanta.
Jika $x=x_{o}\pm\frac{\Delta x}{x_{o}}$,
maka
$kx=kx_{o}\pm\frac{\Delta x}{x_{o}}$
Jika $x=x_{o}\pm\Delta x$,
Jika $x=x_{o}\pm\Delta x$,
maka
$kx=kx_{o}\pm k\Delta x$
10 SOAL DAN PENYELESAIAN KETIDAKPASTIAN PENGUKURAN
10 SOAL DAN PENYELESAIAN KETIDAKPASTIAN PENGUKURAN
