Vektor merupakan besaran yang mempunyai nilai dan arah. Penggambaran vektor berbentuk panah yang menunjukan arah vektor dan panjang garisnya disebut sebagai besar vektor.
10 Soal dan Penyelesaian Pengayaan Vektor Fisika
Soal nomor 1. Sebuah benda mula-mula di titik A (0,0) kemudian bergerak selama 2 sekon ke titik B (4,2), selanjutnya bergerak lagi selama 3 sekon ke titik C (8,6). Kecepatan rata-rata gerak benda adalah (x dan y dalam meter)....
A. 1 m.s-1
B. 1,5 m.s-1
C. 2 m.s-1
D. 2√2 m.s-1
E. 4,75 m.s-1
Penyelesaian Fisika : C
Kita gambarkan Soalnya biar mudah dipahami.
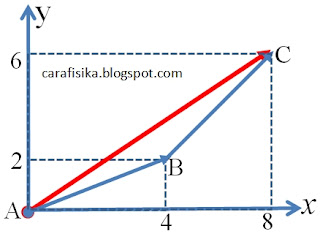Perpindahan AC kita misalkan r.$\small \begin{align*} x&=8i\\y&=6j\\r&=\sqrt{x^2+y^2}\\&=\sqrt{8^2+(6^2}\\&=10\,m\end{align*}$
Kecepatan rata-rata:
$\begin{align*} \bar{v}&=\frac{r}{t}=\frac{10}{2+3}\\&=2\, \, ms^{-1}\end{align*}$
Soal nomor 2. Sebuah truk bergerak ke utara dengan kecepatan 20 m/s kemudian berbelok ke barat dengan kecepatan yang sama. Perubahan kecepatan yang terjadi pada truk tersebut adalah ....
- 40 m/s ke arah barat laut
- 20√2 m/s ke arah barat laut
- 40 m/s ke arah barat daya
- 20√2 m/s ke arah barat daya
- 40 m/s ke arah barat
$\small \begin{align*} &v_x=-20i\\&v_y=20j\\&\textrm{resultan vektor kecepatan:}\\v&=\sqrt{v_x^2+v_y^2}\\v&=\sqrt{(-20)^2+20^2}\\&=20\sqrt 2\,ms^{-1}\\&\textrm{arah vektor resultan:} \\&\tan \theta =\frac{v_y}{v_x}=\frac{20}{-20}=-1\\&\theta =135^o\end{align*}$ Vektor kecepatan $20\sqrt 2\,ms^{-1}$ dengan arah 135o dari Timur ke Utara, berlawanan putaran jam, tepatnya ke Barat Laut.
Soal nomor 3. Nilai maksimum dan minimum dari resultan dua vektor secara berturut – turut adalah 17 unit dan 7 unit. Jika kedua vektor ini saling tegak lurus maka besar resultan vektornya sekarang adalah ....
A. 24
B. 18
C. 15
D. 13
E. 10
Penyelesaian Fisika : D
$\small \begin{align*} A + B = 17&\\ A - B = 7 &+\\\hline 2A=24&\\A=12&\\B=17-12&\\B=5&\end{align*}$
Resultan saat tegak lurus:
$\small \begin{align*} R&=\sqrt{A^2 + B^2} \\&=\sqrt{12^2 + 5^2}\\&=\sqrt {169}=13\textrm{ unit}\end{align*}$
Soal nomor 4. Dua buah gaya masing-masing $F_1 = 3i + bj$ dan $F_2 = 9i + 12j$ bekerja pada sebuah benda yang sama. (i dan j adalah vektor unit sepanjang sumbu +x dan sumbu +y). Agar besar resultan gaya yang bekerja pada benda bernilai minimum, maka besar b adalah ....
A. 0
B. -12
C. 9
D. -10
E. 4
Penyelesaian Fisika : B
Agar resultan vektor bernilai minimum, maka kedua vektor harus berlawanan arah, maka:
$\begin{align*}bj&=-12j\\b&=-12\end{align*}
Soal nomor 5. Seorang anak berdiri di tepi sungai (titik A), ia ingin pergi ke seberang (titik B) dengan menggunakan sebuah perahu. Jika kecepatan aliran air sungai sebesar vs seperti yang ditunjukkan pada gambar berikut.
Kecepatan minimum perahu relatif terhadap aliran sungai agar anak tersebut sampai di titik B adalah ....A. $2\sqrt2v_s$
B. $2v_s$
C. $\sqrt2v_s$
D. $\frac12\sqrt2v_s$
E. $\frac{v_s}{2}$
Penyelesaian Fisika : D
Ada dua kemungkinan yang dapat dilakukan si anak agar bisa sampai di titik B.
- menyeberang dengan arah tegak lurus arus sungai.
- menyeberang dengan arah tertentu melawan arus sungai.
$\begin{align*}v=\sqrt{v_p^2+v_s^2}\end{align*}$
besar kecepatan perahu:
$\begin{align*}\tan 45^o&=\frac{v_p}{v_s}\\1&=\frac{v_p}{v_s}\\v_p&=v_s\end{align*}$
tidak tersedia pada pilihan Soal
Bila menyeberang dengan arah tertentu melawan arus sungai.
Berdasarkan gambar tersebut, kita dapat menghitung:$\small v^2=v_p^2+v_s^2+2v_pv_s\cos(90+\theta)...(1)$
dan
$\small \begin{align*}v_x &=v_s- v_p\cos \theta \\ v_y& = v_p \sin \theta \\&\textrm{sehingga:}\\ v^2&=v_x^2+v_y^2\\v^2&=(v_s-v_p\cos \theta)^2+(v_p\sin\theta)^2\\v^2&=v_s^2-2v_sv_p\cos \theta +v_p^2\cos ^2\theta +v_p^2\sin^2\theta \\v^2&=v_p^2+v_s^2-2v_sv_p\cos \theta ...(2)\end{align*}$
maka:
$\small \begin{align*} v^2&=v_s^2-2v_sv_p\cos \theta +v_p^2 ...(2)\\v^2&=v_p^2+v_s^2+2v_pv_s\cos(90+\theta)...(1)(-)\\ \hline 2&v_sv_p\cos \theta =-2v_pv_s\cos(90+\theta)\\&\cos \theta =-\cos (90^o+\theta)\\&\theta =45^o \end{align*}$
persamaan dapat ditulis:
$\small \begin{align*}v_x &=v_s- v_p\cos \theta \\&=v_s-v_p\cos 45^o\\&=v_s-\frac 12\sqrt{2}v_p\\ v_y& = v_p \sin \theta \\&=v_p\sin 45^o\\&=\frac 12\sqrt{2}v_p\end{align*}$
sehingga:
$\small \begin{align*}\tan \theta &=\frac{v_y}{v_x}\\\tan 45 &=\frac{\frac 12\sqrt{2}v_p}{v_s- \frac 12\sqrt{2}v_p }\\\frac 12\sqrt{2}v_p&=v_s- \frac 12\sqrt{2}v_p \\\sqrt2v_p&=v_s\\v_p&=\frac 12\sqrt{2}v_s\end{align*}$
Soal nomor 6. Sebuah peluru ditembakkan dari meriam di tanah dengan membentuk lintasan parabola. Jika kecepatan peluru saat ditembakkan sebesar (2i + 3j) m/s, maka kecepatan peluru saat tiba di kembali di tanah adalah ....
A. -2i - 3j
B. 2i - 3j
C. -2i + 3j
D. 2i + 3j
E. tidak bisa ditentukan
Penyelesaian Fisika : B
- Komponen kecepatan peluru pada sumbu mendatar adalah tepap, sedangkan pada sumbu vertikal ahakan berubah.
- Saat ditembakkan, $v_o=(2i + 3j) m/s$ maka saat tiba di tanah menjadi: $v_t=(2i - 3j) m/s$
Soal nomor 7. Sebuah vektor p sebesar 5 satuan memiliki arah ke Utara dan vektor q sebesar 12 satuan memiliki arah ke Timur. Jika |p + q| adalah besar dari resultan vektor p + q, pernyataan di bawah ini yang benar adalah ...
A. |p + q| <10
B. |p + q| = 10
C. |p + q| = √17
D. |p + q| = √10
E. |p + q| = 13
Penyelesaian Fisika : E
Arah Timur dan Utara membentuk sudut $90^o$ sehingga kedua vektor saling tegak lurus:
$\small \begin{align*}\left | p+q \right |&=\sqrt{p^2+q^2}\\&=\sqrt{5^2+12^2}\\&=13\textrm{ satuan}\end{align*}$Soal nomor 8. Dua vektor masing-masing $p = 2i + 2j$ dan $q = 2i - 2j$. (i dan j merupakan unit vektor sepanjang sumbu +x dan +y). Sudut yang terbentuk terhadap sumbu x untuk p - q adalah ....
A. 0o
B. 45o
C. -90o
D. 90o
E. -45o
Penyelesaian Fisika : D
$\small \begin{align*}p-q &= (2i + 2j) -(2i - 2j)\\ p - q &= 2i + 2j - 2i + 2j\\p - q &= 4j\end{align*}$
arah vektor p-q:
$\small \begin{align*}p-q &= (2i + 2j) -(2i - 2j)\\ p - q &= 2i + 2j - 2i + 2j\\p - q &= 4j\\ \tan \theta =&\frac{(p - q)_y}{(p - q)_x}\\ \tan \theta =&\frac{4j}{0i}=\textrm{ tdk terdefinisi}\\\theta&=90^o\end{align*}$
Soal nomor 9. Sebuah benda bermassa 2 kg bergerak dalam bidang x-y. Tiba-tiba benda tersebut meledak menjadi 3 keping. Keping pertama dengan massa 0,4 kg bergerak dengan kecepatan v1 = 2i + 3j. Keping kedua dengan massa 0,9 kg bergerak dengan kecepatan v2 = 4i - 2j. Keping ketiga dengan massa 0,7 kg bergerak dengan kecepatan v3 = -5i - 4j. Tentukan vektor kecepatan benda sebelum meledak.
A. 0,45i + 1,7j
B. 0,45i - 1,7j
C. 0,9i - 3,4j
D. 0,9i + 3,4j
E. i - 3j
Penyelesaian Fisika : B
hukum kekekalan momentum untuk sumbu x
$\small \begin{align*}mv_x&=m_1v_{1x}+m_2v_{2x}+m_3v_{3x}\\2v_x&=0,4.2+0,9.4+0,7.(-5)\\2v_x&=0,8+3,6-3,5\\2v_x&=0,9\\v_x&=0,45i\end{align*}$
hukum kekekalan momentum untuk sumbu y
$\small \begin{align*}m v_y &= m_1 v_{1y} + m_2 v_{2y} + m_3 v_{3y}\\ 2 v_y &= 0,4 . 3 + 0,9 . (-2) + 0,7 . (-4)\\ 2 v_y &= 1,2 - 1,8 -2,8\\ 2 v_y &= -3,4\\ v_y &= -1,7 j\end{align*}$
Vektor kecepatan sebelum meledak adalah $\small \begin{align*}v = 0,45i - 1,7j\end{align*}$
Soal nomor 10. Seorang sedang berlari pagi dengan menempuh lintasan seperti pada gambar berikut
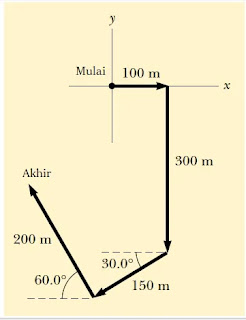Tentukan resultan dan arah perpindahan yang dialami oleh orang tersebut terhadap titik mulainya!Penyelesaian Fisika :
Untuk mempermudah, kita pisahkan semua gaya lalu kita susun pada sumbu xy dengan titik awal berimpit pada koordinat (0,0) lalu kita uraikan semua pada komponen x dan y, sbb:
Komponen sumbu x dan y masing-masing vektor:$\small \begin{align*}S_1&=100m\\S_{1x}&=100m;\,\,S_{1y}=0\\S_2&=300m\\S_{2x}&=0;\,\,S_{2y}=300m\\S_3&=150m\\S_{3x}&=S_3\cos 30^o\\&=150(\frac12\sqrt3)m=75\sqrt3m\\S_{3y}&=S_3\sin 30^o\\&=150(\frac12)=75m\\S4&=200m\\S_{4x}&=S_4\cos 60^o\\&=200(\frac12)m=100m\\S_{4y}&=S_3\sin 60^o\\&=200(\frac12\sqrt3)=100\sqrt3m\end{align*}$
Komponen perpindahan resultan terhadap sumbu x dan sumbu y
$\small \begin{align*}\Sigma S_x& = S_{1x} - S_{3x} - S_{4x}\\&=100-75\sqrt3-100\\&=-75\sqrt3m\end{align*}$
$\small \begin{align*}\Sigma S_y& = S_{4y} - S_{2y} - S_{3y}\\&=100\sqrt3-300-75\\&=100\sqrt3-375\\&=-202m\end{align*}$
Maka resultan perpindahannya adalah
$\small \begin{align*}r&=\sqrt{\Sigma S_x^2+\Sigma S_y^2}\\&=\sqrt{(-75\sqrt3)^2+(-202)^2}\\&=\sqrt{16.875+40.804}\\&=\sqrt{57.679}=240,16m\end{align*}$
Arah perpindahan
$\small \begin{align*}\tan\theta&=\frac{\Sigma S_y}{\Sigma S_x}\\\tan\theta&=\frac{-202}{-75\sqrt3}\textrm{ [kwadran ketiga]}\\\tan\theta&=1,55\\\theta_1&=57,2^o\textrm{ [tidak memenuhi]}\\\theta_2&=180^o+57,2^o=237,2^o\end{align*}$
