Teman Pembaca yang mungkin pernah dihadapkan dengan soal ini, mari sama-sama kita jawab dan mudah-mudahan teman-teman dapat mengerti.
Begini pertanyaannya...
Sebuah balok (massa m) bergerak dengan kelajuan awal $ν_o$ di atas lantai licin. Sebuah batang homogen bermassa M (M jauh lebih besar dari m) dan panjangnya L tergantung dengan bebas pada langit-langit dan mula-mula diam (lihat gambar di bawah). Batang M ditumbuk oleh balok m tersebut.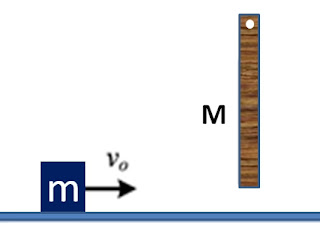
Begini pertanyaannya...
Sebuah balok (massa m) bergerak dengan kelajuan awal $ν_o$ di atas lantai licin. Sebuah batang homogen bermassa M (M jauh lebih besar dari m) dan panjangnya L tergantung dengan bebas pada langit-langit dan mula-mula diam (lihat gambar di bawah). Batang M ditumbuk oleh balok m tersebut.

Tepat setelah tumbukan, batang berayun dan balok diam.
Hukum kekekalan momentum angular, momentum angular (momentum sudut) sebelum dan sesudah tumbukan harus sama. Setelah tumbukan, balok diam sementara itu batang berputar dengan kecepatan sudut ω .
Perhatikan gambar
- Periksalah apakah kasus di atas termasuk tumbukan elastik atau tak-elastik.
- Tentukan tinggi maksimum batang homogen berayun, jika m = 2kg, M = 20kg dan $v_o $= 10m/s.
Hukum kekekalan momentum angular, momentum angular (momentum sudut) sebelum dan sesudah tumbukan harus sama. Setelah tumbukan, balok diam sementara itu batang berputar dengan kecepatan sudut ω .
Perhatikan gambar
Setelah ditumbuk balok, batang berputar dengan sumbu putar salah satu ujungnya, maka momen inersia batang: $\frac13ML^2$.
Dari kekekalan momentum sudut:
$\begin{align*} L_{blk}+L_{btg}&=L'_{blk}+L'_{btg}\\mv_or+0&=0+I\omega \\mv_oL+0&=0+\frac{1}{3}ML^2\omega \\\omega&=\frac{3mv_o}{ML}\end{align*}$
Energi Kinetik:
Sebelum tumbukan, energi kinetik hanya dimiliki balok.$\begin{align*}E_k=\frac12mv_o^2\end{align*}$
Setelah Tumbukan:
$\begin{align*}E'_k&=\frac12I\omega^2\\&=\frac12\left (\frac{1}{3}ML^2 \right )\left ( \frac{3mv_o}{ML} \right )^2\\&=\frac12\left (\frac{1}{3}ML^2 \right )\left ( \frac{9m^2v^2_o}{M^2L^2} \right )\\&=\left ( \frac{3m}{M} \right )\frac12mv_o^2\\&=\left (\frac{3m}{M} \right )E_{ko}\end{align*}$
Karena M jauh lebih besar dari m maka nilai $\frac{3m}{M}$ < 1, maka $E'_k < E_k$, artinya ada energi yang hilang, sehingga tumbukan bersifat tidak elastik.
Tinggi batang terayun:
$\begin{align*}E_A&=E_B\\E_{kA}+E_{pA}&=E_{kB}+E_{pB}\\\left ( \frac{3m}{M} \right )\frac12mv_o^2+0&=0+Mgh \\h=\left ( \frac{3m}{gM^2} \right )&\frac12mv_o^2\\h= \frac{3m^2v_o^2}{2gM^2}&\textrm{ meter}\end{align*}$
Dari kekekalan momentum sudut:
$\begin{align*} L_{blk}+L_{btg}&=L'_{blk}+L'_{btg}\\mv_or+0&=0+I\omega \\mv_oL+0&=0+\frac{1}{3}ML^2\omega \\\omega&=\frac{3mv_o}{ML}\end{align*}$
Energi Kinetik:
Sebelum tumbukan, energi kinetik hanya dimiliki balok.$\begin{align*}E_k=\frac12mv_o^2\end{align*}$
Setelah Tumbukan:
$\begin{align*}E'_k&=\frac12I\omega^2\\&=\frac12\left (\frac{1}{3}ML^2 \right )\left ( \frac{3mv_o}{ML} \right )^2\\&=\frac12\left (\frac{1}{3}ML^2 \right )\left ( \frac{9m^2v^2_o}{M^2L^2} \right )\\&=\left ( \frac{3m}{M} \right )\frac12mv_o^2\\&=\left (\frac{3m}{M} \right )E_{ko}\end{align*}$
Karena M jauh lebih besar dari m maka nilai $\frac{3m}{M}$ < 1, maka $E'_k < E_k$, artinya ada energi yang hilang, sehingga tumbukan bersifat tidak elastik.
Tinggi batang terayun:
$\begin{align*}E_A&=E_B\\E_{kA}+E_{pA}&=E_{kB}+E_{pB}\\\left ( \frac{3m}{M} \right )\frac12mv_o^2+0&=0+Mgh \\h=\left ( \frac{3m}{gM^2} \right )&\frac12mv_o^2\\h= \frac{3m^2v_o^2}{2gM^2}&\textrm{ meter}\end{align*}$
Kita masukkan angka-angkanya, m = 2kg, M = 20kg dan $v_o $= 10m/s.
$\begin{align*}h&= \frac{3m^2v_o^2}{2gM^2}\\&= \frac{3(2)^2(10)^2}{2(10)(20)^2}\\&= \frac{3(400)}{20(400)}\\&=0,15\textrm{ meter}\\&=15\textrm{ cm}\end{align*}$








