Soal dan Penyelesaian Fisika - Latihan soal Ulangan Kenaikan Kelas UKK PAT ini untuk memberikan gambaran mengenai bentuk soal UKK/PAT Fisika pada peserta didik Kelas 10 SMA MA Kurikulum 2013, dibuat berdasarkan kisi-kisi soal materi Fisika SMA MA Kurikulum 2013.
Ulangan Kenaikan Kelas (UKK) atau Penilaian Akhir Tahun (PAT) merupakan salah satu bentuk penilaian hasil belajar sebagai bagian proses pembelajaran agar berlangsung secara efektif dan efisien.
B. 16 m/s
C. 64 m/s
D. 80 m/s
E. 160 m/s
B. 0,25 m
C. 0,40 m
D. 2,50 m
E. 5,00 m
\begin{align*} y=&A\sin (kx-\omega t+\theta )\\15=&15\sin \theta \\\sin \theta =&1\\\theta =& 90^o\\ y=&A\sin (kx-\omega t+\theta )\\y=&15A\sin \left ( \frac{2\pi}{\lambda} x-2\pi f t+\theta \right )\\y=&15\sin \left ( \frac{2\pi}{40} x-2\pi (8)t+90^o \right )\\\pi =&3,14\textrm{ sehingga:}\\y=&15\sin (0,157x-50,2t+90^o )\\\sin &(A+90)=\cos A\\\textrm{maka: }&\\y=&15\sin (0,157x-50,2t+90^o)\\&\textrm{dapat ditulis menjadi:}\\y=&15\cos (0,16x-50,2t)\end{align*}
9. Akibat adanya pemantulan, terbentuk gelombang stasioner dengan persamaan $y = 0,5 \sin (0,4\pi x) \cos \pi (10t-4)$ meter. Berdasarkan persamaan tersebut, cepat rambat gelombangnya adalah .....
Soal UKK PAT Fisika kelas 10
1. Berikut merupakan sifat-sifat gelombang longitudinal.- Terdiri atas bukit dan lembah.
- Terdiri atas rapatan dan renggangan.
- Arah getarnya tegak lurus dengan arah rambatnya.
- Arah getarnya sejajar dengan arah rambatnya.
A. 1 dan 2
B. 1 dan 3
C. 2 dan 3
D. 2 dan 4
E. 4 saja
B. 1 dan 3
C. 2 dan 3
D. 2 dan 4
E. 4 saja
Penyelesaian Fisika:
Sifat-sifat gelombang longitudinal:
- Arah rambat sejajar (berimpit) dengan arah getarnya.
- Berupa rapatan dan renggangan.
- Satu panjang gelombang merupakan jarak satu rapatan dan satu renggangan atau jarak antara dua rapatan yang berdekatan atau jarak antara dua renggangan yang berdekatan.
- Satu panjang gelombang adalah jarak antara rapatan dengan rapatan atau antara renggangan dengan renggangan berikutnya.
- Tidak mengalami polarisasi
2. Perhatikan pernyataan-pernyataan berikut!
A. 1, 2, dan 3
B. 1, 2, dan 4
C. 1, 3, dan 5
D. 2, 3, dan 4
E. 2, 4, dan 5
- Terjadi pemantulan
- Terjadi difraksi
- Mengalami dispersi
- Mengalami polarisasi
A. 1, 2, dan 3
B. 1, 2, dan 4
C. 1, 3, dan 5
D. 2, 3, dan 4
E. 2, 4, dan 5
Penyelesaian Fisika:
Gelombang bunyi adalah gelombang longitudinal dengan sifat-sifat:
- Arah rambat sejajar (berimpit) dengan arah getarnya.
- Berupa rapatan dan renggangan.
- Satu panjang gelombang merupakan jarak satu rapatan dan satu renggangan atau jarak antara dua rapatan yang berdekatan atau jarak antara dua renggangan yang berdekatan.
- Satu panjang gelombang adalah jarak antara rapatan dengan rapatan atau antara renggangan dengan renggangan berikutnya.
- Tidak mengalami polarisasi
A. 0,2 m dan 100 Hz
B. 0,4 m dan 50 Hz
C. 0,8 m dan 25 Hz
D. 40 m dan 0,50 Hz
E. 80 m dan 0,25 Hz
B. 0,4 m dan 50 Hz
C. 0,8 m dan 25 Hz
D. 40 m dan 0,50 Hz
E. 80 m dan 0,25 Hz
Penyelesaian Fisika:
Jarak dua rapatan terdekat sama dengan 1 panjang gelombang = 40cm=0,4m
Frekuensi \begin{align*}
f=&\frac{v}{\lambda }\\=&\frac{20}{0,4}\\=&50Hz\end{align*}
f=&\frac{v}{\lambda }\\=&\frac{20}{0,4}\\=&50Hz\end{align*}
4. Jarak antara rapatan dan renggangan suatu gelombang longitudinal yang mempunyai periode 1/50 sekon adalah 1,6 m. Cepat rambat gelombang tersebut adalah .....
A. 0,64 m/sB. 16 m/s
C. 64 m/s
D. 80 m/s
E. 160 m/s
Penyelesaian Fisika:
Jarak antara rapatan dan renggangan gelombang longitudinal = setengah panjang gelombang, sehingga panjang gelomgan menjadi 2x1,6 m=3,2 m.
\begin{align*}
v=&\frac{\lambda }{T}\\=&\frac{3,2}{\frac{1}{50}}\\=&160\;ms^{-1}\end{align*}
\begin{align*}
v=&\frac{\lambda }{T}\\=&\frac{3,2}{\frac{1}{50}}\\=&160\;ms^{-1}\end{align*}
5. Suatu gelombang stasioner mempunyai persamaan $y = 0,2 \cos 2\pi x. \sin 10\pi t$ (y dan x dalam meter dan t dalam sekon). Jarak antara perut dan simpul yang berurutan pada gelombang tersebut adalah .....
A. 0,15 mB. 0,25 m
C. 0,40 m
D. 2,50 m
E. 5,00 m
Penyelesaian Fisika:
Jarak perut dan simpul yang berurutan pada gelombang stasioner sama dengan seperempat panjang gelombang. \begin{align*}y = &0,2 \cos {\color{Red} {2\pi x}}. \sin {\color{Blue} {10\pi t}}\\y = &A \cos {\color{Red}{ kx}}. \sin {\color{Blue} {\omega t}}\\&\textrm{diperoleh:}\\k=&2\pi\\\frac{2\pi}{\lambda }=&2\pi \\\lambda =& 1\;m\\0,5\lambda=&0,5\;m\end{align*}6. Diketahui persamaan gelombang berjalan $Y_p = 0,05 \sin (100\pi t - 0,02x)$, dengan y dan x dalam meter, t dalam sekon. Maka :
A. 1, 2, dan 3
B. 1 dan 3
C. 2 dan 4
- Amplitudo gelombang 5 cm
- Frekuensi gelombang 50Hz
- Panjang gelombang 100$\pi $m
- Cepat rambat gelombang 2$\pi $m/s
A. 1, 2, dan 3
B. 1 dan 3
C. 2 dan 4
D. 4 saja
E. 1, 2, 3, dan 4
Penyelesaian Fisika:
\begin{align*} Y_p = &0,05 \sin ( 100\pi t-0,02x)\\ Y_p =& A\sin ( 2\pi ft-( \frac{2\pi }{\lambda } )x)\\&\textrm{didapat:} \\A=&0,05\;m=5\;cm\\2f=&100\Rightarrow f=50\;Hz\\\frac{2\pi}{\lambda}=&0,02\Rightarrow \lambda =100\pi \;m\\v=&f\lambda=50(100\pi)\\=&5000\pi\;m.s^{-1}\end{align*}
7. Sebuah gelombang berjalan mempunyai persamaan simpangan $y = 0,5 \sin \pi (50t + 10x)$ m.Tentukan cepat rambat gelombang tersebut .....
A. 5,0 m/s
B. 11,0 m/s
C. 11,5 m/s
D. 12,5 m/s
E. 13,5 m/s
7. Sebuah gelombang berjalan mempunyai persamaan simpangan $y = 0,5 \sin \pi (50t + 10x)$ m.Tentukan cepat rambat gelombang tersebut .....
A. 5,0 m/s
B. 11,0 m/s
C. 11,5 m/s
D. 12,5 m/s
E. 13,5 m/s
Penyelesaian Fisika:
\begin{align*}y = &0,5 \sin \pi (50t + 10x)\\v=&\frac{\textrm{koefisien t}}{\textrm{koefisien x}}=\frac{50}{10}=5ms^{-1}\end{align*}8. Gelombang sinusoidal bergerak ke arah x-positif. Amplitudo gelombang tersebut adalah 15 cm, panjangnya 40 cm dan frekuensinya 8 Hz. Jika posisi vertikal dari elemen medium pada t = 0 dan x = 0 adalah 15 cm, maka bentuk umum fungsi gelombangnya adalah.....
Saat t = 0 dan x = 0 simpangan y=15 cm- $\small {y=15\sin (0,16x+50,2t-\frac{\pi}{2})}$
- $\small y=15\sin (0,16x+50,2t+\frac{\pi}{2})$
- $\small y=15\sin (0,16x+50,2t)$
- $\small y=15\cos (0,16x-50,2t-\frac{\pi}{4})$
- $\small y=15\cos (0,16x+50,2t)$
\begin{align*} y=&A\sin (kx-\omega t+\theta )\\15=&15\sin \theta \\\sin \theta =&1\\\theta =& 90^o\\ y=&A\sin (kx-\omega t+\theta )\\y=&15A\sin \left ( \frac{2\pi}{\lambda} x-2\pi f t+\theta \right )\\y=&15\sin \left ( \frac{2\pi}{40} x-2\pi (8)t+90^o \right )\\\pi =&3,14\textrm{ sehingga:}\\y=&15\sin (0,157x-50,2t+90^o )\\\sin &(A+90)=\cos A\\\textrm{maka: }&\\y=&15\sin (0,157x-50,2t+90^o)\\&\textrm{dapat ditulis menjadi:}\\y=&15\cos (0,16x-50,2t)\end{align*}
9. Akibat adanya pemantulan, terbentuk gelombang stasioner dengan persamaan $y = 0,5 \sin (0,4\pi x) \cos \pi (10t-4)$ meter. Berdasarkan persamaan tersebut, cepat rambat gelombangnya adalah .....
A. 2 m/s
B. 4 m/s
C. 5 m/s
B. 4 m/s
C. 5 m/s
D. 10 m/s
E. 25 m/s
Penyelesaian Fisika:
\begin{align*} y =& 0,5 \sin (0,4\pi x) \cos \pi (10t-4)\\v=&\frac{\textrm{koefisien t}}{\textrm{koefisien x}}=\frac{10}{0,4}=25ms^{-1}\end{align*}10. Gelombang stasioner dapat terjadi karena superposisi gelombang datang dan gelombang pantul oleh ujung bebas. Titik simpul yang kedelapan berjarak 2,25 m dari ujung bebasnya. Jika frekuensi gelombang tersebut adalah 80 Hz, maka cepat rambat gelombangnya adalah .....
A. 72 m/s
B. 64 m/s
C. 48 m/s
D. 32 m/s
E. 16 m/s
A. 72 m/s
B. 64 m/s
C. 48 m/s
D. 32 m/s
E. 16 m/s
Penyelesaian Fisika:
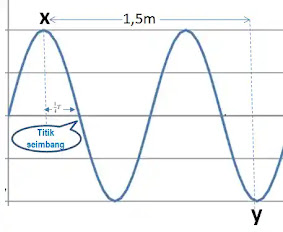
\begin{align*}X_{10} =& \frac{(2n-1)\lambda }{4}\\2,25 =& (2(8)-1)\frac{\lambda }{4}\\2,25 =& 15/4 \lambda \\2,25 =& 3,75 \lambda \\\lambda =& 2,52/3,75\\\lambda =& 0,6 m\end{align*}Jadi Laju Rambat Gelombang :\begin{align*}V =& f x \lambda \\ =& 80 \times 0,6\\ =& 48 m/s\end{align*}11. Suatu pagi, Dimpun melihat dua gabus x dan y terapung di danau. Gabus tersebut terpisah sejauh 1,5m, ketika gelombang sinusoida menjalar pada permukaan air teramati pada saat t = 0 sekon gabus x berada di puncak gelombang sedangkan gabus y berada di lembah gelombang. Kedua gabus tersebut dipisahkan satu puncak gelombang. Pada saat t = 1 sekon, gabus x berada di titik seimbang pertama kali dan sedang bergerak turun. Berdasarkan informasi tersebut, pernyataan yang benar tentang kasus tersebut adalah.....
\begin{align*}1\frac{1}{2}\lambda =&1,5\Rightarrow \lambda=1\;m\\\frac{1}{4}T=&1\Rightarrow T=4\;s\\T=&\frac{1}{f}\Rightarrow 4=\frac{1}{f}\\f=&\frac{1}{4}=0,25\;Hz\end{align*}
12. Seutas senar panjangnya 4m dengan kedua ujung yang terikat erat. Senar tersebut selanjutnya diberikan getaran sehingga terbentuk 8 buah perut, maka letak perut kelima dari ujung terjauh adalah…
dengan menggunakan cara perbandingan
8 perut = 4 gelombang = 4 meter, sehingga:$4\lambda=4m\\\lambda = 1 \;m$
Perut ke-5 dari ujung terjauh adalah 2,25 gelombang
maka, $P_5=2,25\lambda = 2,25(1)=2,25\;m$
\begin{align*} TI_1=&10\log \frac{I_1}{I_o}\\=&10\log \frac{10^{-4}}{10^{-12}}\\=&10\log 10^8\\=&80\;dB\\ I\approx \frac{1}{r^2}\\\frac{I_1}{I_2}=&\left ( \frac{r_2}{r_1} \right )^2\\\frac{10^{-4}}{I_2}=&\left ( \frac{3}{6} \right )^2=\frac{1}{4}\\I_2=&4.10^{-4}\;Wm^{-2}\\TI_2=&10\log \frac{I_2}{I_o}\\=&10\log \frac{4.10^{-4}}{10^{-12}}\\=&10\log 4.10^8\\=&10\log 2^2+10\log10^8\\=&20\log 2+10\log10^8\\=&20(0,3)+80\\=&86\;dB\\ \frac{TI_2}{TI_1}=& \frac{86}{80}\\=&\frac{44}{40}\end{align*}.- Gelombang air memiliki panjang 200 cm.
- Frekuensi gelombang adalah 0,25 Hz.
- Balok x akan kembali berada di puncak pada saat t = 4,5 sekon.
- Pada saat t = 1 sekon, balok y berada di titik seimbang dan sedang bergerak turun.
- Amplitudo gelombang adalah 75 cm.
Perhatikan gambar berikut:
12. Seutas senar panjangnya 4m dengan kedua ujung yang terikat erat. Senar tersebut selanjutnya diberikan getaran sehingga terbentuk 8 buah perut, maka letak perut kelima dari ujung terjauh adalah…
A. 1,5 m
B. 1,75 m
C. 2 m
D. 2,25 m
E. 2,5 m
Penyelesaian Fisika:
Gelombang stasioner ujung terikat:dengan menggunakan cara perbandingan
8 perut = 4 gelombang = 4 meter, sehingga:$4\lambda=4m\\\lambda = 1 \;m$
Perut ke-5 dari ujung terjauh adalah 2,25 gelombang
maka, $P_5=2,25\lambda = 2,25(1)=2,25\;m$
Dengan rumus:\begin{align*} P_n=&\frac{(2n-1)\lambda}{4} \\=&\frac{(2(5)-1)\times 1}{4} =2,25\;m\end{align*} 13. Sebuah sumber bunyi A adalah mengeluarkan nada dengan frekuensi P dan didengar oleh pendengar B. Saat A dan B diam di tempatnya masing-masing, B mendengar nada itu dengan frekuensi Q, kemudia B bergerak mendekati A sehingga nada yang didengarnya berfrekuensi R. Setelah melewati A, nada yang didengar B berfrekuensi S. Hubungan frekuensi P, Q, R, dan S dinyatakan sebagai .....
Keadaan I, A dan B diam di tempatnya masing-masing. A mengeluarkan nada dengan frekuensi P dan B mendengar nada itu dengan frekuensi Q. Hubungan frekuensi yang di dengar A dan B:
\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{P}{Q}=&\frac{v+0}{v+0}\\v+0=&v+0\\\textrm{ maka: } &P=Q\end{align*} Keadaan II, B bergerak mendekati A sehingga nada yang didengarnya berfrekuensi R. Hubungan frekuensi yang di dengar A dan B:\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{R}{P}=&\frac{v+v_p}{v+0}\\(v+v_p)&>v+0\\\textrm{maka:} &R>P\end{align*}Keadaan III, setelah melewati A, nada yang didengar B berfrekuensi S. Hubungan frekuensi yang di dengar A dan B:\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{S}{P}=&\frac{v-v_p}{v+0}\\(v-v_p)&<(v+0)\\\textrm{maka: }\\&S<P\end{align*}Hubungan frekuensi P, Q, R dan S dinyatakan sebagai $P = Q, R > P, S < P.$
A. P = Q = R = S
B. Q = P, R > P, S > P
C. Q = P, R > P, S < P
D. Q = P, R < P, S > P
E. Q < P, R < P, S < P
B. Q = P, R > P, S > P
C. Q = P, R > P, S < P
D. Q = P, R < P, S > P
E. Q < P, R < P, S < P
Penyelesaian Fisika:
Perhatikan gambar berikut:
\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{P}{Q}=&\frac{v+0}{v+0}\\v+0=&v+0\\\textrm{ maka: } &P=Q\end{align*} Keadaan II, B bergerak mendekati A sehingga nada yang didengarnya berfrekuensi R. Hubungan frekuensi yang di dengar A dan B:\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{R}{P}=&\frac{v+v_p}{v+0}\\(v+v_p)&>v+0\\\textrm{maka:} &R>P\end{align*}Keadaan III, setelah melewati A, nada yang didengar B berfrekuensi S. Hubungan frekuensi yang di dengar A dan B:\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{S}{P}=&\frac{v-v_p}{v+0}\\(v-v_p)&<(v+0)\\\textrm{maka: }\\&S<P\end{align*}Hubungan frekuensi P, Q, R dan S dinyatakan sebagai $P = Q, R > P, S < P.$
14. Telinga manusia hanya mampu menerima intensitas bunyi terbesar sebesar 1 $W.m^2$. Hal ini menunjukkan bahwa.....
B. 810 Hz
C. 815 Hz
- manusia dapat mendengar bunyi dengan intensitas minimal 1 $W.m^2$.
- ambang rasa sakit manusia adalah 120 dB.
- manusia hanya dapat mendengar bunyi dengan intensitas 1 $W.m^2$.
- ambang rasa sakit manusia adalah 1 dB.
- ambang rasa sakit manusia adalah 10 dB.
Penyelesaian Fisika:
Batas intensitas bunyi yang dapat didengar telinga manusia normal adalah sebagai berikut:
- Intensitas terendah sebesar $10^{-12}W.m^2$. Batas ini disebut sebagai intensitas ambang pendengaran.
- Intensitas tertinggi yang dapat didengar tanpa rasa sakit di telinga sebesar $1\;W.m^2$. Batas ini disebut sebagai intensitas ambang perasaan.
- Interval intensitas bunyi yang dapat didengar oleh telinga normal manusia adalah $10^{-12}W.m^2$ hingga $1\;W.m^2$. Taraf intensitas (TI) bunyi adalah nilai logaritma perbandingan antara intensitas bunyi dengan intensitas ambang pendengaran dan dinyatakan dalam decibel (dB).
15. Seorang siswa sedang diam di halte depan sekolahnya untuk menunggu jemputan, siswa tersebut mendengar bunyi mobil yang berbeda ketika mobil mendekat dan menjauhinya. Mobil tersebut mengeluarkan bunyi sebesar 800 Hz. Jika kecepatan bunyi di udara 340 m/s sedangkan kecepatan mobil 20 m/s, maka frekuensi yang didengar saat mobil mendekat adalah.....
A. 805 Hz B. 810 Hz
C. 815 Hz
D. 850 Hz
E. 875 Hz
Penyelesaian Fisika:
\begin{align*} \frac{f_{p}}{f_{s}}=&\frac{v\pm v_p}{v\pm v_s}\\\frac{f_{p}}{800}=&\frac{340+0}{340-20}\\f_p=& \frac{800(340)}{320}=850\;Hz\end{align*}16. Dua orang anak-anak dipisahkan jarak sejauh r. Jika jarak anak pertama ke sumber bunyi adalah 3 kali jarak anak kedua ke sumber bunyi tersebut, maka perbandingan intensitas bunyi yang diterima anak pertama dan anak kedua adalah .....
A. 1 : 3
B. 1 : 9
C. 1 : 12
B. 1 : 9
C. 1 : 12
D. 3 : 1
E. 9 : 1
Penyelesaian Fisika:
\begin{align*} I\approx &\frac{1}{r^2}\\\frac{I_1}{I_2}=&\left ( \frac{r_2}{r_1} \right )^2\Rightarrow r_1=3r_2\\\frac{I_1}{I_2}=&\left ( \frac{r_2}{3r_2} \right )^2=\frac{1}{9}\end{align*} 17. Suatu titik yang berjarak 6 m dari sumber bunyi memiliki intensitas $10^{-4} watt.m^{-2}$. Jika titik tersebut digeser mendekati sumber bunyi sejauh 3 m, perbandingan taraf intensitas setelah digeser dengan sebelum digeser adalah .....(log 2 =0,3)
A. 3 : 2
B. 5 : 3
C. 5 : 11
A. 3 : 2
B. 5 : 3
C. 5 : 11
D. 8 : 17
E. 43 : 40
Penyelesaian Fisika:
Penyelesaian Fisika:
