Program linear digunakan secara luas di bidang matematika dan secara khusus di bidang bisnis, ekonomi, dan teknologi. Industri pun menerapkan program linear, seperti transportasi, pengelolaan energi, telekomunikasi, dan manufaktur. Program linier terbukti mampu memecahkan masalah perencanaan, penjadwalan, dan desain.
SOAL DAN PENYELESAIAN PROGRAM LINIER KELAS 11
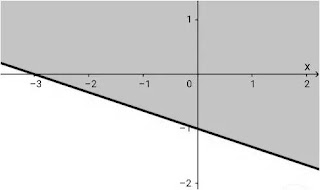
Soal Nomor 1 . Perhatikan grafik berikut!
Daerah yang diarsir merupakan Penyelesaian dari pertidaksamaan ...
A. $3y + x \geq-3$
B. $3y + x \leq-3$
C. $3y + x \leq 3$
D. $3x + y \geq-3$
E. $3y- x \leq 3$
Penyelesaian: A
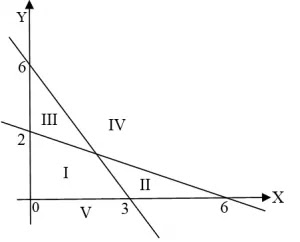
Soal Nomor 2. Daerah Penyelesaian: dari sistem pertidaksamaan linear
$\begin{cases} 2x+y & \leq 6 \\ x + 3y & \geq 6 \\ x & \geq 0 \\ y & \geq 0 \end{cases}$untuk $x, y$ anggota bilangan real adalah ...
A. I
B. II
C. III
D. IV
E. V
Penyelesaian: C
Soal Nomor 3. Perhatikan grafik di bawah ini.
A. $3y + x \geq-3$
B. $3y + x \leq-3$
C. $3y + x \leq 3$
D. $3x + y \geq-3$
E. $3y- x \leq 3$
Penyelesaian: A
- Grafik garis lurus di atas memotong sumbu-X di (-3, 0) dan memotong sumbuY di (0,-1). Dengan demikian, persamaan garisnya berbentuk
$\begin{align*}-1x + (-3)y & = (-1)(-3) \\-x- 3y & = 3 \\ 3y + x & =-3 \end{align*}$ - Uji titik (0, 0) untuk mengecek tanda: $0 + 3(0) = 0 \geq-3$
- Dengan demikian, pertidaksamaan garisnya adalah ${3y + x \geq-3}$
Soal Nomor 2. Daerah Penyelesaian: dari sistem pertidaksamaan linear
$\begin{cases} 2x+y & \leq 6 \\ x + 3y & \geq 6 \\ x & \geq 0 \\ y & \geq 0 \end{cases}$untuk $x, y$ anggota bilangan real adalah ...
A. I
B. II
C. III
D. IV
E. V
Penyelesaian: C
- Titik potong garis $2x + y \leq 6$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.
$\begin{array}{|c|c|c|} \hline x & 0 & 3 \\ \hline y & 6 & 0 \\ \hline (x, y) & (0,6) & (3, 0) \\ \hline \end{array}$ - Daerah I dan II adalah daerah Penyelesaian: untuk pertidaksamaan ini karena bertanda $\leq$ (arsirannya ke bawah).
- Titik potong garis $x+3y \geq 6$ terhadap sumbu koordinat dapat dinyatakan dalam tabel berikut.
$\begin{array}{|c|c|c|} \hline x & 0 & 6 \\ \hline y & 2 & 0 \\ \hline (x, y) & (0,2) & (6, 0) \\ \hline \end{array}$ - Daerah III dan IV adalah daerah Penyelesaian: untuk pertidaksamaan ini karena bertanda $\geq$ (arsirannya ke atas).
- Perhatikan bahwa pertidaksamaan $x \geq 0, y \geq 0$ membatasi daerah Penyelesaiannya hanya pada kuadran pertama.
Soal Nomor 3. Perhatikan grafik di bawah ini.

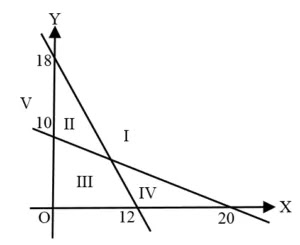
Daerah Penyelesaian dari sistem pertidaksamaan $3x+2y \leq 36$; $x + 2y \geq 20$; $x \geq 0$ dan $y \geq 0$ pada gambar di atas adalah ...A. V
B. IV
C. III
D. II
E. I
B. IV
C. III
D. II
E. I
Penyelesaian: D
Soal Nomor 4. Perhatikan gambar berikut!
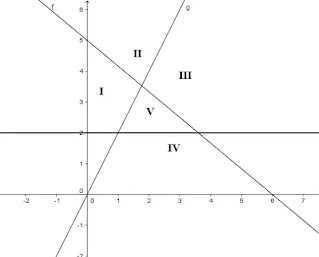
Daerah Penyelesaian sistem pertidaksamaan $5x + 6y \geq 30$; $-2x + y \leq 0$, $y \geq 2$ ditunjukkan oleh daerah ...
A. I
B. II
- Grafik dari pertidaksamaan $3x + 2y \leq 36$ memotong sumbu X di x = 12 dan memotong sumbu Y di y = 18. Karena bertanda $\leq$, maka arsiran daerah Penyelesaian: nya ke bawah, yaitu daerah II, III, dan V.
- Grafik dari pertidaksamaan $x + 2y \geq 20$ memotong sumbu X di x = 20 dan memotong sumbu Y di y = 10. Karena bertanda $\geq$, maka arsiran daerah Penyelesaian: nya ke atas, yaitu daerah I, II, dan V.
- (x, y) juga bertanda nonnegatif. Ini berarti, daerah penyelesainnya hanya termuat di kuadran pertama. Dengan demikian, daerah Penyelesaian sistem pertidaksamaan tersebut adalah daerah II.
Soal Nomor 4. Perhatikan gambar berikut!

Daerah Penyelesaian sistem pertidaksamaan $5x + 6y \geq 30$; $-2x + y \leq 0$, $y \geq 2$ ditunjukkan oleh daerah ...
A. I
B. II
C. III
D. IV
E. V
Penyelesaian: C
Gambar garis $5x + 6y \geq 30$ dengan memanfaatkan titik potong terhadap sumbu koordinat.
$\begin{array}{|c|c|c|} \hline x & 0 & 6 \\ \hline y & 5 & 0 \\ \hline (x, y) & (0, 5) & (6, 0) \\ \hline \end{array}$
Jadi, garis melalui titik $(0, 5)$ dan $(6, 0)$. Uji titik $(0, 0)$ pada $5x + 6y \geq 30$, sehingga diperoleh $0 + 0 = 0 \geq 30$ (bernilai salah), sehingga daerah Penyelesaian: nya tidak meliputi titik $(0, 0)$.

Daerah Penyelesaian meliputi daerah II dan III.
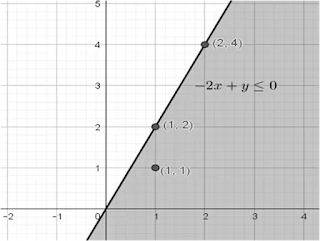
Selanjutnya, gambar garis $-2x + y \leq 0$ dengan menentukan dua titik yang dilalui garis
$\begin{array}{|c|c|c|} \hline x & 1 & 2 \\ \hline y & 2 & 4 \\ \hline (x, y) & (1, 2) & (2, 4) \\ \hline \end{array}$
Jadi, garis melalui titik $(1, 2)$ dan $(2, 4)$. Uji titik $(1, 1)$ pada $-2x + y \leq 0$, sehingga diperoleh $-2(1) + 1 =-1 \leq 0$ (bernilai benar), sehingga daerah Penyelesaian: nya meliputi titik $(1, 1)$
Gambar garis $5x + 6y \geq 30$ dengan memanfaatkan titik potong terhadap sumbu koordinat.
$\begin{array}{|c|c|c|} \hline x & 0 & 6 \\ \hline y & 5 & 0 \\ \hline (x, y) & (0, 5) & (6, 0) \\ \hline \end{array}$
Jadi, garis melalui titik $(0, 5)$ dan $(6, 0)$. Uji titik $(0, 0)$ pada $5x + 6y \geq 30$, sehingga diperoleh $0 + 0 = 0 \geq 30$ (bernilai salah), sehingga daerah Penyelesaian: nya tidak meliputi titik $(0, 0)$.

Daerah Penyelesaian meliputi daerah II dan III.
Selanjutnya, gambar garis $-2x + y \leq 0$ dengan menentukan dua titik yang dilalui garis
$\begin{array}{|c|c|c|} \hline x & 1 & 2 \\ \hline y & 2 & 4 \\ \hline (x, y) & (1, 2) & (2, 4) \\ \hline \end{array}$
Jadi, garis melalui titik $(1, 2)$ dan $(2, 4)$. Uji titik $(1, 1)$ pada $-2x + y \leq 0$, sehingga diperoleh $-2(1) + 1 =-1 \leq 0$ (bernilai benar), sehingga daerah Penyelesaian: nya meliputi titik $(1, 1)$
.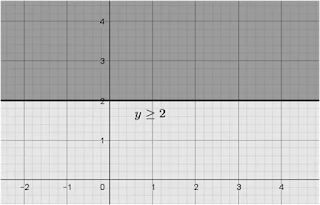
Daerah Penyelesaian: meliputi daerah I, II, III, dan V.
Daerah yang terkena ketiga arsiran daerah Penyelesaian di atas adalah daerah III.
Soal Nomor 6. Sistem pertidaksamaan linear untuk daerah yang diarsir pada gambar di bawah adalah ...
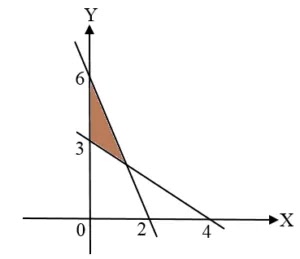
A. $3x + 4y \geq 12; 3x+y \leq 6; x \geq 0; y \geq 0$
B. $3x + 4y \leq 12; 3x+y \geq 6; x \geq 0; y \geq 0$
C. $3x + 4y \geq 12; x+y \leq 6; x \leq 0; y \geq 0$
D. $3x + 4y \leq 12; 3x+y \leq 6; x \geq 0; y \geq 0$
E. $3x + 4y \geq 12; 3x+y \geq 6; x \geq 0; y \geq 0$
Penyelesaian: A
Soal Nomor 7. Daerah yang diarsir pada grafik di bawah merupakan himpunan Penyelesaian: sistem pertidaksamaan ...

Daerah Penyelesaian: meliputi daerah I, II, III, dan V.
Daerah yang terkena ketiga arsiran daerah Penyelesaian di atas adalah daerah III.
Soal Nomor 6. Sistem pertidaksamaan linear untuk daerah yang diarsir pada gambar di bawah adalah ...

A. $3x + 4y \geq 12; 3x+y \leq 6; x \geq 0; y \geq 0$
B. $3x + 4y \leq 12; 3x+y \geq 6; x \geq 0; y \geq 0$
C. $3x + 4y \geq 12; x+y \leq 6; x \leq 0; y \geq 0$
D. $3x + 4y \leq 12; 3x+y \leq 6; x \geq 0; y \geq 0$
E. $3x + 4y \geq 12; 3x+y \geq 6; x \geq 0; y \geq 0$
Penyelesaian: A
- Persamaan garis yang memotong sumbu X di x = 4 dan sumbu Y di y = 3 adalah $3x + 4y = 12$. Tanda ketaksamaan yang sesuai dengan daerah arsiran adalah $\geq$ karena arsirannya di atas garis, sehingga diperoleh pertidaksamaan linear $3x+4y \geq 12$
- Persamaan garis yang memotong sumbu X di x = 2 dan sumbu Y di y = 6 adalah $6x + 2y = 12$ atau disederhanakan menjadi $3x+y = 6$.
- Tanda ketaksamaan yang sesuai dengan daerah arsiran adalah $\leq$ karena arsirannya di bawah garis, sehingga diperoleh pertidaksamaan linear $3x+y \leq 6$.
- Karena daerah arsiran terletak di kuadran pertama, maka kendala non-negatif ($x, y$ tak boleh bernilai negatif) diberlakukan.
- Jadi, sistem pertidaksamaan linearnya adalah $\begin{cases} 3x + 4y \geq 12 \\ 3x + y \leq 6 \\ x \geq 0 \\ y \geq 0 \end{cases}$
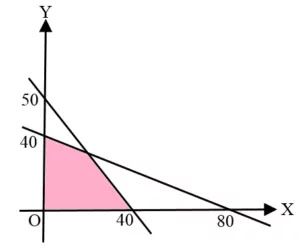
Soal Nomor 7. Daerah yang diarsir pada grafik di bawah merupakan himpunan Penyelesaian: sistem pertidaksamaan ...

$\begin{align*} & \text{A}. 5x + 4y \leq 200; 2x + y \leq 80; x \geq 0, y \geq 0 \\ & \text{B}. 5x + 4y \geq 200; x + 2y \leq 80; x \geq 0, y \geq 0 \\ & \text{C}. 4x + 5y \leq 200; 2x + y \leq 80; x \geq 0, y \geq 0 \\ & \text{D}. 4x + 5y \leq 200; 2x + y \geq 80; x \geq 0, y \geq 0 \\ & \text{E}. 5x + 4y \leq 200; x + 2y \leq 80; x \geq 0, y \geq 0 \end{align*}$
Penyelesaian: E
Soal Nomor 8. Daerah Penyelesaian: yang memenuhi sistem pertidaksamaan $x \geq 2$; $y \leq 8$, $x-y \leq 2$ berbentuk ...
A. segitiga lancip
B. segitiga sama sisi
C. segitiga sebarang
D. segitiga tumpul sama kaki
E. segitiga siku-siku sama kaki
Penyelesaian: E
- Persamaan garis pertama: $50x + 40y = 50 . 40 = 2000$, disederhanakan menjadi ${5x + 4y = 200}$.
- Titik $(0, 0)$ merupakan salah satu himpunan Penyelesaian dari pertidaksamaan tersebut (perhatikan arsirannya), sehingga diperoleh ${5x + 4y \leq 200}$
- Persamaan garis kedua: $40x + 80y = 40 . 80 = 3200$, disederhanakan menjadi ${x + 2y = 80}$.
- Titik $(0, 0)$ merupakan juga salah satu himpunan Penyelesaian dari pertidaksamaan tersebut (perhatikan arsirannya), sehingga diperoleh ${x + 2y \leq 80}$
- Kendala non-negatif diberikan oleh $x \geq 0$ dan $y \geq 0$ karena daerah Penyelesaiannya hanya memuat kuadran pertama.
- Jadi, sistem persamaan sesuai dengan daerah Penyelesaian yang diberikan tersebut adalah ${5x + 4y \leq 200; x + 2y \leq 80; x \geq 0; y \geq 0}$
Soal Nomor 8. Daerah Penyelesaian: yang memenuhi sistem pertidaksamaan $x \geq 2$; $y \leq 8$, $x-y \leq 2$ berbentuk ...
A. segitiga lancip
B. segitiga sama sisi
C. segitiga sebarang
D. segitiga tumpul sama kaki
E. segitiga siku-siku sama kaki
Penyelesaian: E
Gambarkan grafik pertidaksamaan pada sistem koordinat Kartesius seperti gambar.
Daerah yang diarsir merupakan daerah Penyelesaian .
Gambarkan grafik pertidaksamaan pada sistem koordinat Kartesius seperti gambar.
Daerah yang diarsir merupakan daerah Penyelesaian .

Tampak bahwa daerah Penyelesaianberbentuk segitiga siku-siku sama kaki ($AB = BC = 8$).
Soal Nomor 9. Perhatikan gambar berikut ini!
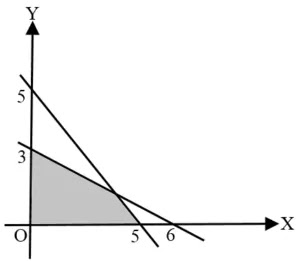
Nilai maksimum untuk fungsi objektif $P = 3x + 5y$ adalah ...
A. 15
Soal Nomor 9. Perhatikan gambar berikut ini!

Nilai maksimum untuk fungsi objektif $P = 3x + 5y$ adalah ...
A. 15
B. 17
C. 19
D. 16
D. 16
E. 18
Penyelesaian: B
- Daerah Penyelesaian itu memiliki 3 titik pojok. Salah satunya adalah titik potong kedua garis itu. Koordinat titik potongnya dapat dicari dengan menggunakan metode Penyelesaian: SPLDV. Persamaan garis yang dimaksud dituliskan dalam sistem persamaan linear dua variabel berikut. $\begin{cases} 5x + 5y & = 25 \Rightarrow x + y = 5 \\ 3x + 6y & = 18 \Rightarrow x + 2y = 6 \end{cases}$
- Dengan menggunakan metode gabungan (eliminasi-substitusi) pada SPLDV, diperoleh $\begin{align*} & x + y = 5 \\ & x + 2y = 6 \\ \hline &-y =-1 \\ & y = 1 \end{align*}$
- Substitusikan $y = 1$ pada persamaan pertama, $\begin{align*} x + y & = 5 \\ x + 1 & = 5 \\ x & = 4 \end{align*}$
- Jadi, titik potongnya ada di koordinat $(4, 1)$.
- Koordinat titik pojok daerah Penyelesaian tersebut adalah $(0, 3), (4, 1)$, dan $(5, 0)$. Uji titik ini pada fungsi objektif $P = 3x + 5y$.
- Dari tabel di atas, nilai maksimum fungsi objektif $P = 3x+5y$ adalah ${17}$
$\begin{array}{|c|c|} \hline \text{Titik Pojok} & P = 3x+5y \\ \hline (0, 3) & 15 {(4, 1)} & {17} \\ (5, 0) & 15 \\ \hline \end{array}$
Soal Nomor 10. Perhatikan grafik berikut!

Nilai minimum dari $Z=2x+5y$ dari daerah yang diarsir adalah ...
A. 6
B. 8
C. 10
D. 11
E. 14
Penyelesaian: B
A. 6
B. 8
C. 10
D. 11
E. 14
Penyelesaian: B
Daerah Penyelesaian itu memiliki 3 titik. Salah satunya adalah titik potong kedua garis itu. Koordinat titik potongnya dapat dicari dengan menggunakan metode Penyelesaian SPLDV. Persamaan garis yang dimaksud dituliskan dalam sistem persamaan linear dua variabel berikut.
$\begin{cases} 6x + 3y & = 18 \Rightarrow 2x + y = 6 \\ 4x + 4y & = 16 \Rightarrow x + y = 4 \end{cases}$
Dengan menggunakan metode gabungan (eliminasi-substitusi) pada SPLDV, diperoleh $\begin{align*} 2x + y& = 6 \\ x + y &= 4(-) \\ \hline x &= 2 \end{align*}$
Substitusikan $x = 2$ pada persamaan kedua,
$\begin{align*} x + y & = 4 \\ 2 + y & = 4 \\ y & = 2 \end{align*}$
Jadi, titik potongnya ada di koordinat $(2, 2)$.
Koordinat titik sudut daerah Penyelesaian tersebut adalah $(4, 0), (2, 2)$, dan $(0, 6)$. Uji titik ini pada fungsi objektif $Z=2x+5y$.
$\begin{array}{|c|c|} \hline \text{Titik Sudut} & Z=2x+5y \\ \hline { (4, 0)} & {8} \\ (2, 2) & 14 \\ (0, 6) & 30 \\ \hline \end{array}$
Dari tabel di atas, nilai minimum fungsi objektif $Z=2x+5y$ adalah 8
$\begin{cases} 6x + 3y & = 18 \Rightarrow 2x + y = 6 \\ 4x + 4y & = 16 \Rightarrow x + y = 4 \end{cases}$
Dengan menggunakan metode gabungan (eliminasi-substitusi) pada SPLDV, diperoleh $\begin{align*} 2x + y& = 6 \\ x + y &= 4(-) \\ \hline x &= 2 \end{align*}$
Substitusikan $x = 2$ pada persamaan kedua,
$\begin{align*} x + y & = 4 \\ 2 + y & = 4 \\ y & = 2 \end{align*}$
Jadi, titik potongnya ada di koordinat $(2, 2)$.
Koordinat titik sudut daerah Penyelesaian tersebut adalah $(4, 0), (2, 2)$, dan $(0, 6)$. Uji titik ini pada fungsi objektif $Z=2x+5y$.
$\begin{array}{|c|c|} \hline \text{Titik Sudut} & Z=2x+5y \\ \hline { (4, 0)} & {8} \\ (2, 2) & 14 \\ (0, 6) & 30 \\ \hline \end{array}$
Dari tabel di atas, nilai minimum fungsi objektif $Z=2x+5y$ adalah 8