 SOAL DAN PENYELESAIAN TOPIK GERAK HARMONIK SEDERHANA
SOAL DAN PENYELESAIAN TOPIK GERAK HARMONIK SEDERHANA
Soal 1. Seseorang hendak menghitung percepatan jatuh bebas ditempat ia berada. Ia melakukan eksperimen dengan mengayunkan sebuah bandul yang digantung pada seutas tali 30 cm. Ia mengukur bahwa waktu rata-rata untuk melakukan 10 ayunan adalah 11 detik. Dari data ini hitung berapa percepatan jatuh bebas di tempat percobaan?
Penyelesaian Fisika:
Untuk melakukan 10 ayunan diperlukan waktu 11 detik, jadi 1 ayunan memerlukan perioda: \begin{align*}T=\frac{t}{n}=\frac{11}{10}\,s\end{align*}Besar percepatan gravitasi berdasarkan percobaan adalah:\begin{align*}T& =2\pi \sqrt {\frac {l}{g}}\\T^2& =4\pi^2\left (\frac {l}{g} \right )\\g&=\frac {4\pi ^2l}{T^2}=\frac {4(3,14) ^2(0,3)}{\left ( \frac{11}{10} \right ) ^2}\\g&=\frac{1183,152}{121}\approx 9,78\,ms^{-2}\end{align*}
Soal 2. Carilah panjang bandul sederhana jika periodenya 5 s pada titik dimana g bernilai 9,8 m/s2
Soal 2. Carilah panjang bandul sederhana jika periodenya 5 s pada titik dimana g bernilai 9,8 m/s2
Penyelesaian Fisika:
\begin{align*}T& =2\pi \sqrt {\frac {l}{g}}\\T^2& =4\pi^2\left (\frac {l}{g} \right )\\l&=\frac {gT^2}{4\pi ^2}=\frac {(9,8)5^2}{4(3,14) ^2}\\l&=\frac{245,25}{39,43}\approx 6,22m\end{align*}
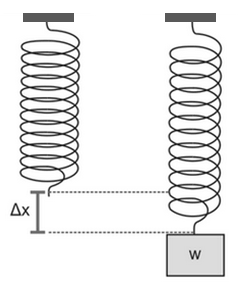
Soal 3. Sebuah pegas bertambah panjang 10 cm jika diberi beban 100 N. Jika suatu benda bermassa 2 kg diikatkan pada pegas itu lalu digetarkan, berapa periode ayunan pegas itu?
Penyelesaian Fisika: \begin{align*}T& =2\pi \sqrt {\frac {m}{k}}\Rightarrow k=\frac {F}{\Delta y}\\&maka:\\T& =2\pi \sqrt {\frac {m}{\frac {F}{\Delta y}}}=2\pi \sqrt {\frac {m.\Delta y}{F}}\\T& =2\pi \sqrt {\frac {2.(0,1)}{100}}\\T& =2(3,14) \sqrt {\frac {2}{1000}}\\T&=0,8\,s
\end{align*}
Soal 4. Sebuah ayunan bergetar dengan periode 1,5 sekon. Apabila amplitudo ayunan sebesar 10 cm, simpangan ayunan setelah bergetar selama 4 sekon adalah...
\begin{align*}T& =2\pi \sqrt {\frac {l}{g}}\\T^2& =4\pi^2\left (\frac {l}{g} \right )\\l&=\frac {gT^2}{4\pi ^2}=\frac {(9,8)5^2}{4(3,14) ^2}\\l&=\frac{245,25}{39,43}\approx 6,22m\end{align*}
Soal 3. Sebuah pegas bertambah panjang 10 cm jika diberi beban 100 N. Jika suatu benda bermassa 2 kg diikatkan pada pegas itu lalu digetarkan, berapa periode ayunan pegas itu?
Penyelesaian Fisika: \begin{align*}T& =2\pi \sqrt {\frac {m}{k}}\Rightarrow k=\frac {F}{\Delta y}\\&maka:\\T& =2\pi \sqrt {\frac {m}{\frac {F}{\Delta y}}}=2\pi \sqrt {\frac {m.\Delta y}{F}}\\T& =2\pi \sqrt {\frac {2.(0,1)}{100}}\\T& =2(3,14) \sqrt {\frac {2}{1000}}\\T&=0,8\,s
\end{align*}
Soal 4. Sebuah ayunan bergetar dengan periode 1,5 sekon. Apabila amplitudo ayunan sebesar 10 cm, simpangan ayunan setelah bergetar selama 4 sekon adalah...
Penyelesaian Fisika:\begin{align*}y& = A \sin \omega t\\y& = A \sin \left (\frac {2\pi t}{T} \right ) |_{t=4}\\y& = 10 \sin \left (\frac {2\pi (4) }{1,5} \right ) \\y& = 10 \sin \left (\frac {16\pi }{3} \right )\\y& = 10 \sin \left (\frac {2\pi }{3} \right )\\y& = 10 \sin 120^o\\y& = 10 (0,5\sqrt{3}\\y&=5\sqrt{3}\,cm\end{align*}
Soal 5. Sebuah benda melakukan gerak harmonis dengan periode 0,8 detik. Jika benda bergerak dari keadaan setimbang dan amplitudo A, maka saat t=1 detik simpangan benda tersebut adalah... kali amplitudonya.
Penyelesaian Fisika:\begin{align*}y& = A \sin \omega t\\y& = A \sin \left (\frac {2\pi }{T} \right ) t\\y& = A \sin \left (\frac {2\pi }{0,8} \right ) (1)\\y& = A \sin \left (2,5\pi \right )\\y& = A \sin (0,5\pi)=A(1) \\y& = A \end{align*}Simpangannya sama dengan Amplitudonya.
Soal 6.Sebuah partikel memiliki simpangan x yang memenuhi $x = 0,4 \cos \pi(3t+\frac{1}{4})$ dengan x dalam meter dan t dalam sekon, hitunglah frekuensi f getaran.
Penyelesaian Fisika:\begin{align*} x&=0,4\cos \pi(3t+\frac {1}{4})\\x&=0,4\cos (3\pi t+\frac {\pi}{4})\\x&=A\cos (\omega t+\theta )\\&diperoleh:\\\omega &=3\pi\\2\pi f&=3\pi\\f&=\frac {3}{2}=1,5Hz\end{align*}
Soal 7. Sebuah partikel memiliki simpangan x yang memenuhi $x = 0,4 \cos \pi(3t+\frac{1}{4})$ dengan x dalam meter dan t dalam sekon, carilah posisi partikel pada saat t = 0 sekon.
Penyelesaian Fisika:\begin{align*}x&=0,4\cos \pi(3t+\frac {1}{4})|_{t=0}\\x&=0,4\cos \pi(3(0)+\frac {1}{4})\\x&=0,4\cos (\frac {\pi}{4})\\x&=0,4\cos 45^o\\x&=0,4(0,5\sqrt{2})\\x&=0,2\sqrt{2})m\\x&=20\sqrt{2})cm\end{align*}
Soal 8. Sebuah partikel mengalami gerak harmonik sederhana dengan persamaan gerak dinyatakan sebagai berikut : $y = 10 \sin (10\pi t + \pi/6)$. Jika y dalam cm dan t dalam detik, tentukan simpangan atau posisi getaran ketika t = 1 sekon.
Penyelesaian Fisika:\begin{align*}y& = 10 \sin (10\pi t + \pi/6)|_{t=1}\\y& = 10 \sin (10\pi (1) + \pi/6)\\y &= 10 \sin (\frac {\pi}{6})\\y &= 10 \sin 30^o\\y &= 10 (0,5)=5cm\end{align*}
Soal 9. Diketahui persamaan simpangan gerak harmonik sederhana: $y = 6 \sin (2\pi t + \pi/6) $ y dalam cm dan t dalam sekon. Hitunglah kecepatan getar partikel pada saat pertama sekali simpangannya 3 cm.
Penyelesaian Fisika:\begin{align*}y&={\color{Blue} A}\sin ({\color{Red} \omega} t+{\color{Magenta} \theta})\\ y &={\color{Blue} 6 }\sin ({\color{Red} {2\pi}} t + {\color{Magenta} {\pi/6}})\\&diperoleh:\\
A&=6cm\\\omega &=2\pi \\\theta &=\pi/6=30^o\end{align*}maka:\begin{align*} y &=6 \sin (2\pi t + \pi/6)|_{y=3} \\3&=6 \sin (2\pi t + 30^o)\\0,5&= \sin (2\pi t + 30^o)\\\sin 30^o&= \sin (2\pi t + 30^o)
\\ 30^o&= 2\pi t + 30^o\\2\pi t&=0\\t &=0\end{align*}kecepatan partikel: \begin{align*} v &=A\omega \cos (\omega t + \theta )\\v &=A(2\pi ) \cos (2\pi t + 30^o ) \\v &=6(2\pi ) \cos (2\pi (0) + 30^o ) \\v &=12\pi \cos 30^o\\v &=12\pi (0,5\sqrt{3})\\v &=6\pi \sqrt{3}\,cm.s^{-1}\end{align*}
Soal 10. Posisi partikel diberikan oleh : $x = 5 \cos 4 \pi t$ dengan x dalam cm dan t dalam sekon. Kapankah setelah t = 0 partikel pertama kali berada pada posisi kesetimbangannya?
Penyelesaian Fisika:
Partikel berada pada posisi setimbang ketika x=0; \begin{align*} x&=5 \cos 4 \pi t\\0&=5 \cos 4 \pi (t)\\0&= \cos 4 \pi (t)\\\cos \frac {\pi}{2}&= \cos 4 \pi (t)\\\frac{1}{2}&=4t\\t&=\frac{1}{8}\, s\end{align*}
11. Soal yang Anda cari mungkin di sini:
- Soal dan penyelesaian getaran atau gerak harmonik sederhana
- Soal dan penyelesaian materi elastisitas dan hukum hooke kelas xi
- 20 soal dan penyelesaian - elastisitas dan gerak harmonik sederhana
- Gerak harmonik sederhana atau getaran







