KAPASITOR KEPING SEJAJAR
Soal Dan Penyelesaian Fisika SMA - Kapasitor atau condensator adalah suatu komponen elektronika yang terdiri dari dua buah penghantar yang diberi sekat lalu diberi muatan yang sama besar tetaoi berlainan tanda.Sekat tersebut terbuat dari bahan isolasi (mika, kertas, keramik, udara, dan sebagainya), yang berfungsi untuk memperbesar kapasitas kapasitor tersebut.
Satuan dari kapasitansi kondensator adalah Farad (F). Namun Farad adalah satuan yang terlalu besar, sehingga digunakan:
- Pikofarad pF=10-12F
- Nanofarad nF=10-9F
- Microfarad μF=10-6F
Kapasitas kapasitor keping sejajar dituliskan dalam persamaan sebagai berikut:\[ C = k\frac{A.\varepsilon o}{d}\]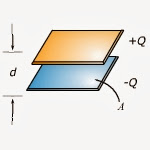
1. Luas penampang keping penghantar
2. Jarak antar keping
3. Jenis dielektrika
Satuan dari kapasitansi kondensator adalah Farad (F). Namun Farad adalah satuan yang terlalu besar, sehingga digunakan:
- Pikofarad pF=10-12F
- Nanofarad nF=10-9F
- Microfarad μF=10-6F
Kapasitas kapasitor keping sejajar dituliskan dalam persamaan sebagai berikut:\[ C = k\frac{A.\varepsilon o}{d}\]

Dalam hal ini,
- C = kapasitas kapasitor
- εo=permitivitas ruang hampa
- k= konstanta dielektrikum ( untuk udara/hampa = 1 ),
- A = luas bidang plat
- d = jarak antara plat
1. Luas penampang keping penghantar
2. Jarak antar keping
3. Jenis dielektrika
RANGKAIAN KAPASITOR
Rangakian Kapasitor dibagi menjadi dua yaitu rangakain seri dan rangkaian paralel. Cara penghitungannya hampir sama dengan rangakian seri dan paralel pada resistor. Berikut ini persamaan dari rangkaian kapasitor.1. Rangkaian Seri
Rangkaian seri pada kapasitor merupakan rangkaian kapasitor dengan menghubungkan kutub TIDAK sejenis antara kapasitor, seperti yang diperlihatkan pada gambar berikut ini :Kapasitas pengganti pada rangkaian seri adalah:
$ \frac{1}{C_{tot}}= \frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}} \\ Q_{tot}=Q_{1}=Q_{2}=Q_{3} \\ V_{tot}=V_{1}+V_{2}+V_{3}$

$ \frac{1}{C_{tot}}= \frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}} \\ Q_{tot}=Q_{1}=Q_{2}=Q_{3} \\ V_{tot}=V_{1}+V_{2}+V_{3}$
2. Rangakian Paralel
Rangkaian paralel merupakan rangkaian kapasitor dengan menghubungkan kutub SEJENIS antara kapasitor, seperti yang diperlihatkan pada gambar berikut ini:
Kapasitas pengganti pada rangkaian paralel adalah :
$C_{tot}=C_{1}+C_{2}+C_{3} \\ Q_{tot}=Q_{1}+Q_{2}+Q_{3} \\ V_{tot}=V_{1}=V_{2}=V_{3}$
3. Energi Kapsitor
Muatan listrik menimbulkan potensial listrik dan untuk memindahkannya diperlukan usaha. Untuk memberi muatan pada suatu kapasitor diperlukan usaha listrik, dan usaha listrik ini disimpan di dalam kapasitor sebagai energi. Pemberian muatan dimulai dari nol sampai dengan Q coulomb. Persamaan Energi pada kapasitor dapat ditulis : \[W=\frac{1}{2}CV^{_{2}} \\ W=\frac{1}{2}QV \\ W=\frac{1}{2}\frac{Q^{2}}{C}\]keterangan :
W = energi kapasitor(J)
Q = Muatan Listrik (C)
V = Potensial listrik(V)
Jawaban dari Pak Dimpun:
Andaikan Kapasitor dibuat berbentuk KUBUS, maka:
\[\small C=A\frac{\varepsilon _{o}}{d} \Rightarrow A = d^{2}\]maka\[\small C=d.\varepsilon _{o} \\ d=\frac{C}{\varepsilon _{o}}\\d= \frac{1}{8,85.10^{-12}}\\d \approx 113.10^{^{9}}m \\d= 113.10^{6}km.\] Volume Kapasitor:\[\small V=d^{3}=(113.10^{6})^{3}km^{3} \approx 1,44.10^{24}km^{3} \] Volume Bumi: \[\small V\approx 1,08.10^{12}km^{3}\]Perbandingan Volume Capasitor dengan Volume Bumi adalah:\[\small \frac{V{_{c}}}{V_{b}}\\V= 1,33.10^{12}.\] Artinya, kapasitor memiliki volume 1,33.1012 kali volume Bumi. Kalau begitu, mungkinkah dibuat kapasitor plat sejajar berisi udara dengan kapasitas 1 F? Bagaimana pendapat anda?
02. Jika kapasitas masing-masing kapasitor adalah C, maka kapasitas total rangkaian di bawah ini dari titik A ke titik B adalah.....

Jawaban dari Pak Dimpun:

$C_{tot}=C_{1}+C_{2}+C_{3} \\ Q_{tot}=Q_{1}+Q_{2}+Q_{3} \\ V_{tot}=V_{1}=V_{2}=V_{3}$
3. Energi Kapsitor
Muatan listrik menimbulkan potensial listrik dan untuk memindahkannya diperlukan usaha. Untuk memberi muatan pada suatu kapasitor diperlukan usaha listrik, dan usaha listrik ini disimpan di dalam kapasitor sebagai energi. Pemberian muatan dimulai dari nol sampai dengan Q coulomb. Persamaan Energi pada kapasitor dapat ditulis : \[W=\frac{1}{2}CV^{_{2}} \\ W=\frac{1}{2}QV \\ W=\frac{1}{2}\frac{Q^{2}}{C}\]keterangan :
W = energi kapasitor(J)
Q = Muatan Listrik (C)
V = Potensial listrik(V)
SOAL DAN PENYELESAIAN LISTRIK STATIS: RANGKAIAN KAPASITOR
01. Mungkinkah dibuat kapasitor plat sejajar berisi udara dengan kapasitas 1 F?Jawaban dari Pak Dimpun:
Andaikan Kapasitor dibuat berbentuk KUBUS, maka:
\[\small C=A\frac{\varepsilon _{o}}{d} \Rightarrow A = d^{2}\]maka\[\small C=d.\varepsilon _{o} \\ d=\frac{C}{\varepsilon _{o}}\\d= \frac{1}{8,85.10^{-12}}\\d \approx 113.10^{^{9}}m \\d= 113.10^{6}km.\] Volume Kapasitor:\[\small V=d^{3}=(113.10^{6})^{3}km^{3} \approx 1,44.10^{24}km^{3} \] Volume Bumi: \[\small V\approx 1,08.10^{12}km^{3}\]Perbandingan Volume Capasitor dengan Volume Bumi adalah:\[\small \frac{V{_{c}}}{V_{b}}\\V= 1,33.10^{12}.\] Artinya, kapasitor memiliki volume 1,33.1012 kali volume Bumi. Kalau begitu, mungkinkah dibuat kapasitor plat sejajar berisi udara dengan kapasitas 1 F? Bagaimana pendapat anda?
02. Jika kapasitas masing-masing kapasitor adalah C, maka kapasitas total rangkaian di bawah ini dari titik A ke titik B adalah.....

Jawaban dari Pak Dimpun:

Sebelum kita menjawab soal di atas, mari kita sebentar berandai-andai. Andaikata kamu punya tali yang panjangnya tak hingga, terus saya potong satu centimeter Apakah panjangnya masih tak hingga? Saya yakin kita sepakat dengan jawaban; Ya! tali itu tetap panjangnya tak hingga.
Sekarang, kalau total kapasitas dari A ke B kita sebut $\small C_{AB}$, dan sedikit dari rangkaian saya potong (lihat gambar diatas) maka rangkaian yang tertinggal akan tetap memiliki kapasitas sebesar $C_{AB}$ (analogi tali diatas).
Sekarang rangkaian itu menjadi:

Mari kita hitung $C_{AB}$:
Kapasitor C seri dengan ( $\small C_{AB}$ paralel C) \[\small C_{AB}=\frac{C(C_{AB}+C)}{C+(C_{AB}+C)} \\ \small CC_{AB}+C^{2}=2CC_{AB}+C_{AB}^{2} \\ \small C_{AB}^{2}+CC_{AB}-C^{2}=0\] \[\small C_{AB}=\frac{-C\pm\sqrt{C^{2}-4.1(-C^{2})}}{2.1} \\ \small C_{AB}= \frac{C\sqrt{5}-C}{2}=\frac{1}{2}C(\sqrt{5}-1)=0,618C\]
SELAMAT BELAJAR.
Sekarang, kalau total kapasitas dari A ke B kita sebut $\small C_{AB}$, dan sedikit dari rangkaian saya potong (lihat gambar diatas) maka rangkaian yang tertinggal akan tetap memiliki kapasitas sebesar $C_{AB}$ (analogi tali diatas).
Sekarang rangkaian itu menjadi:

Mari kita hitung $C_{AB}$:
Kapasitor C seri dengan ( $\small C_{AB}$ paralel C) \[\small C_{AB}=\frac{C(C_{AB}+C)}{C+(C_{AB}+C)} \\ \small CC_{AB}+C^{2}=2CC_{AB}+C_{AB}^{2} \\ \small C_{AB}^{2}+CC_{AB}-C^{2}=0\] \[\small C_{AB}=\frac{-C\pm\sqrt{C^{2}-4.1(-C^{2})}}{2.1} \\ \small C_{AB}= \frac{C\sqrt{5}-C}{2}=\frac{1}{2}C(\sqrt{5}-1)=0,618C\]
SELAMAT BELAJAR.








