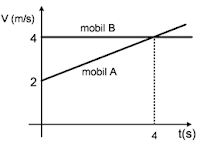
01. Dua mobil A dan B bergerak melalui jalan yang sama dan berangkat dari titik awal yang sama secara bersamaan. Kurva kecepatan v kedua mobil sebagai fungsi waktu t diberikan pada gambar di bawah.
Tentukan:- persamaan jarak tempuh A dan B sebagai fungsi dari waktu.
- kapan dan di mana mobil A berhasil menyusul mobil B.
- sketsa kurva posisi kedua mobil terhadap waktu dalam satu gambar. Ambil selang waktu sejak kedua mobil berangkat hingga sesaat setelah mobil A menyusul mobil B.
- Jika setelah menempuh jarak 60 m mobil A melambat dengan besar perlambatan yang sama dengan besar percepatan ketika awal perjalanan, kapan dan di manakah mobil B berhasil menyusul mobil A?
a. Persamaan jarak tempuh A dan B sebagai fungsi dari waktu.
Mobil B bergerak lurus beraturan, dengan kecepatan 4 m/s. Persamaannya jarak tempuhnya adalah: \[\\S=V.t\\\\S=4t\]
Mobil A bergerak lurus berubah beraturan, dengan kecepatan awal Vo = 2 m/s dan saat t = 4 s, kecepatannya adalah 4 m/s.
Percepatan mobil A:
\[\\V_{t} = V_{o} + at\\ 4 = 2 + 4a\\ a = 0,5 ms^{-2}\]Persamaan jarak untuk mobil A: \[\\S = V_{o}t + \frac{1}{2}at^{2}\\\\ S = 2t + \frac{1}{2}.0,5.t^{2}\\\\ S = 2t + \frac{1}{4}t^{2}\] b.Mobil A menyusul B: \[\\4t=2t+\frac{1}{4}t^{2}\\\\ 16t=8t+t^{2}\\\\ t^{2}-8t=0\\\\ t(t - 8) = 0\\\\ t = 8 s\] Pada jarak: S = 4t = 4(8) = 32 meter
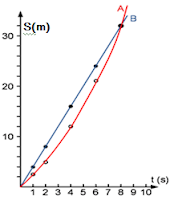
c. Sketsa kurva posisi kedua mobil terhadap waktu.
Mobil B: S = 4
t = 1 s → S = 4(1) = 4 m
t = 2 s → S = 4(2) = 8 m
t = 4 s → S = 4(4) = 16 m
t = 8 s → S = 4(8) = 32 m
Mobil A:$S=2t+0,25.t^{2}$
t = 1 s → S = 2(1) + 0,25(1)2 = 2,25 m
t = 2 s → S = 2(2) + 0,25(2)2 = 5 m
t = 4 s → S = 2(4) + 0,25(4)2 = 12 m
t = 8 s → S = 2(8) + 0,25(8)2 = 32 m
Grafik:
d. Mobil B berhasil menyusul mobil A
Waktu yang diperlukan mobil A menempuh 60 m adalah:\[\\S = 2t+\frac{1}{4}t^{2}\\ 60 = 2t+\frac{1}{4}t^{2}\\t^2+ 8t - 240 = 0\\ (t + 20)(t - 12) = 0\]
Ambil t = 12 sekon.
Jarak tempuh A dan B masing-masing saat t = 12 s adalahSoB = 60 m
SoB = 4t = 4(12) = 48 m
Kecepatan mobil A dan B masing-masing t = 12 s adalah:
VA = Vo + at
VA = 2 + (0,5)12 = 8 m/s menjadi Vo untuk gerak sejak diperlambat
VB= 4 m/s konstan
Waktu yang diperlukan mobil B menyusul mobil A sejak diperlambat adalah
\[\\S_{A}= S_{B}\\\\S_{oA}+ V_{oA}t-\frac{1}{2}at^{2} = S_{oB}+V_{B}t\\\\60 + 8t-\frac{1}{2}.0,5t^{2} = 48 + 4t\\\\12 + 4t - \frac{1}{4}t^{2} = 0\\\\t^{2}- 16t - 48 = 0\\\\t^{2}- 16t - 48 = 0\\\\t=\frac{-(-16)\pm \sqrt{(-16)^{2}-4.1.(-48)}}{2}\\\\t=(8+4\sqrt{7})\]Dalam waktu (8 + 4√7) sekon tersebut jarak tempuh B adalah:
SB=VB.t=4(8 + 4√7) = (32 + 16√7) meter.
Sehingga total waktu yang diperlukan adalah:
12 + (8 + 4√7) = (20 + 4√7) sekon
pada jarak 48 + (32 + 16√7) = (80 + 16√7) m atau sekitar 122,33 m.
Jarak tempuh mobil A dari mulai diperlambat untuk t = (8 + 4√7) sekon: \[\\S = V_{o}t-\frac{1}{2}at^{2}\\\\ S=8(8+4\sqrt{7})-\frac{1}{2}(8+4\sqrt{7})\\\\S=148,66-86,33\approx 62,33 m\]Jarak dihitung dari awal gerak dengan demikian adalah 60 + 62,33 = 122,33 m
02. Sebuah bola berada di atas sebuah tiang vertikal (lihat gambar).
Tiba-tiba bola tersebut pecah menjadi dua bagian. Satu bagian terpental mendatar ke kiri dengan kecepatan 3 m/s dan satu bagian lagi terpental ke kanan dengan kecepatan 4 m/s. Pada kondisi tertentu vektor kecepatan dari dua pecahan tersebut saling tegak lurus. Bila g = 10 m.s-2, Hitung :a. watu yang dibutuhkan setelah tumbukan hingga kondisi itu tercapai,
b. jarak antara kedua pecahan itu saat kondisi di atas terjadi.
Jawaban Fisika dari Pak Dimpun:
Vektor kecepatan masing-masing pecahan (kanan (+), kiri (-))\[\\v^{_{1}}=(-3i-v_{y}j)\\v^{_{2}} = (4i-v_{y}j)\] Kedua vektor saling tegak lurus saat v1 ⋅ v2 = 0 sehingga\[\\(-3i - v_{y}j).(4i - v_{y}j)=0\\ -12+v_{y}^{2} = 0 \\v_{y}^{2} = 12\\ v_{y} = 2\sqrt{3}\] a) Waktu yang diperlukan dari gerak jatuh bebas pada sumbu y:\[\\v_{y} = g.t\\\\2\sqrt{3} = 10t\\\\t=\frac{1}{5}\sqrt{3}sekon\] b) Jarak kedua pecahan ditentukan dari gerakan pada sumbu x\[\\\Delta x = x_{2} - x_{1}\\\Delta x = v_{2x}t - v_{1x}t\\\Delta x = (v_{2x} - v_{1x})t\\\Delta x = (4-(-3))\frac{1}{5}\sqrt{3}\\\Delta x = \frac{7}{5}\sqrt{3} m\]Free Download buku [DOWNLOAD]
Selamat belajar
