Rumus momen inersia partikel dapat dilihat seperti di bawah ini.\[I=\Sigma mr^{2}\]dimana:
- I menunjukkan momen inersia (kgm2),
- r merupakan jarak tegak lurus suatu benda yang diputar terhadap sumbu putar, dan
- m adalah massa benda (kg).
- dm adalah elemen massa dari benda yang dihitung, dan
- r adalah jarak dari elemen massa terhadap sumbu putar.
Dalam banyak kasus sering kali sumbu putar benda homogen tidak tepat dipusat benda tetapi mengalami pergeseran pada jarak tertentu. Untuk menghitung momen inersia yang telah mengalami pergeseran dapat digunakan teorema sumbu sejajar, yang dapat dituliskan sebagai berikut:\[\small I=I_{p}+md^{2}\]
- I merupakan momen inersia pada sumbu tertentu,
- m menunjukkan massa benda, dan
- d merupakan jarak dari sumbu pusat ke sumbu putar yang baru.
1. Banyak molekul dalam tubuh manusia seperti molekul yang mempunyai kemiripan dengan molekul diatomik seperti terlihat pada gambar di bawah ini.

Massa A adalah 3 kg dan massa B adalah 5 kg, serta jarak antara B dengan sumbu putar adalah 2m. Tentukanlah momen inersia sistem terhadap sumbu putar yang terlihat pada gambar!
Jawaban Fisika Pak Dimpun
Momen inersia total terhadap sumbu putar adalah \begin{align*} I&=I_{A}+I_{B}\\ I&=m_{A}r_{A}^{2}+m_{B}r_{B}^{2}\\ I&=(3)(1)^{2}+(5)(2)^{2}=23kgm^{2}\end{align*}
2. Sebuah sistem kawat berbentuk segiempat yang panjang sisinya 4 m x 3m terlihat seperti pada gambar di bawah ini. Pada setiap ujung kawat disimpan beban dengan massa beban yang berurutan dari A, B, C, D yaitu 1 kg, 2 kg, 3kg dan 4 kg.
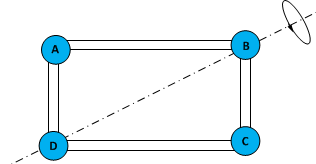
Jika sistem diputar seperti terlihat pada gambar di atas yang memelwati massa B dan D, tentukanlah momen inersia sistem tersebut!
Jawaban Fisika Pak Dimpun
Pertama kita cari jarak benda A dan C ke sumbu putar,berdasarkan gambar berikut, benda yang memeliki momen inersia adalah benda A dan C karena memiliki jarak terhadap sumbu putar. Jaraknya diperlihatkan seperti pada gambar di bawah ini.
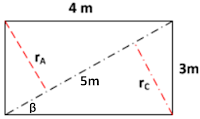
Jarak benda A dan C terhadap sumbu putar adalah \begin{align*} \sin \beta =\frac{3}{5}&=\frac{r_{C}}{4}\\\\r_{A}=r_{c}&=\frac{12}{5}\end{align*}
Momen inersia sistem di atas adalah
\begin{align*} I&=I_{A}+I_{C}\\I&=m_{A}r_{A}^{2}+m_{c}r_{c}^{2}\\ I&=(1)\left ( \frac{12}{5}\right )^{2}+(3)\left (\frac{12}{5} \right )^{2}\\I&=23.0kgm^{2}\end{align*}
3: Sebuah batang homogen yang panjangnya L diputar pada bagian tengah dari panjangnya seperti terlihat pada gambar di bawah ini.

Tentukanlah momen inersia batang jika panjang batang L dan massa batang tersebut M (anggap kerapatan batang homogen atau seragam)!
Jawaban Fisika Pak Dimpun
Karena ini benda homogen atau kerapatan seragam dan benda ini bersifat kontinu, momen inersia benda dapat dihitung dengan persamaan momen inersia untuk benda kontinu. Misalkan kita mengambil elemen massa dm sepanjang dx. Besar dm = A dx. Dimana A adalah A = M/L atau rapat massa linier. Jadi momen inersia sistem adalah \begin{align*} I&=2\int_{0}^{L/2}r^{2}dm\\\\I&=2\int_{0}^{L/2}x^{2}(A dx)\\\\I&=(2)\frac{1}{3}Ax^{3}\mid _{0}^{L/2}\\\\I&=\frac{AL^{3}}{12}\end{align*} Dengan mengganti A dengan M/L, akan didapatkan persamaan momen inersia sebagai berikut: \begin{align*} I=\frac{mL^{2}}{12} \end{align*}
4: Sebuah batang yang panjangnya L dan bermassa M memiliki momen inersia $\small I=\frac{mL^{2}}{12}$ ketika diputar pada tengah-tengah batang. Tentukanlah momen inersia batang jika diputar pada salah satu ujung batang (gunakan teorema sumbu sejajar)!
Jawaban Fisika Pak Dimpun
Dalam menghitung momen inersia yang telah diketahui momen inersia disumbu pusat putarnya. Momen inersia akan lebih mudah dihitung dengan teorema sumbu sejajar meskipun dengan cara meninjau elemen massa pun dapat dilakukan.
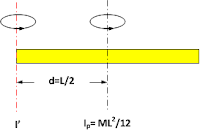
Momen inersia pada ujung batang adalah \begin{align*} I'&=I_{p}+Md^{2}\\ I&=\frac{ML^{2}}{12}+M\left ( \frac{L}{2} \right )^{2}\\I&=\frac{4ML^{2}}{12}=\frac{ML^{2}}{3} \end{align*}







