SOAL DAN PENYELESAIAN HUKUM NEWTON PADA KATROL
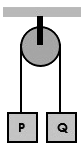
1. Pada katrol yang massanya diabaikan, digantungkan seutas tali yang pada ujung-ujungnya digantungkan beban P dan Q seperti gambar, jika mP = 6 kg, mQ = 14 kg dan g=10m/s².
Tentukan:
- Besar percepatan masing-masing benda
- Tegangan tali T1 dan T2
- Jika benda mula-mula dalam keadaan diam, hitunglah kecepatan benda setelah bergerak 2 detik!
Karena beban Q lebih besar maka Q akan bergerak turun dan beban P bergerak naik.
a. percepatan masing-masing benda
$a=\frac{\Delta m.g}{m_{A}+m_{B}}\\a=\frac{(14-6)10}{14+6}\\a=\frac{80}{20}=4ms^{-2}$
percepatan masing-masing benda adalah 4 m/s²
b. Tegangan tali
$T=2(\frac{m_{A}.m_{B}}{m_{A}+m_{B}})g\\T=2(\frac{14.6}{14+6})10\\ T=84N$
c. kecepatan sesaat
Benda mula-mula dalam keadaan diam maka kecepatan awal benda = 0. Setelah bergerak selama 2 detik kecepatan akhir benda yaitu:
$v_{t} = v_{o} + a.t\\ v_{t} = 0 + 4 (2)\\ v_{t} = 8 ms^{-1}$
2.Dua benda A dan B masing-masing 2 kg dan 3 kg dihubungkan dengan tali melalui katrol seperti gambar berikut.
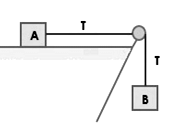
Jika gesekan antara tali dengan katrol diabaikan serta benda B bergerak turun, hitunglah besar percepatan dan tegangan tali T jika:
- Gesekan benda A dengan lantai diabaikan (lantai licin)
- Koefisien gesekan kinetis antara balok A dengan lantai 0,2
a. percepatan saat bidang licin
$a=\frac{m_{B}.g}{m_{A}+m_{B}}\\a=\frac{3.10}{2+3}=6ms^{-2}$
Tegangan tali TA dan TB
$T= m_{1}a=2.6=12N$
TA=TB = T = maka tegangan talinya = 12 N
b. percepatan dan tegangan tali jika lantai kasar
$a=\frac{(m_{B}-\mu m_{A})g }{m_{A}+m_{B}}\\a=\frac{(3-0,2.2.)10}{2+3}=\frac{26}{5}=5,2ms^{-2}$
$T_{A} = m_{A}a + f_{A}\\T_{A} = m_{A}a + \mu .m_{A}g\\T_{A} = 2(5,2) + 0,2.2.10\\T_{A} =14,4N$
TA=TB = T = maka tegangan talinya = 14,4 N
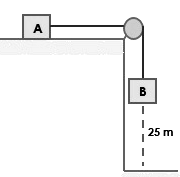
3. Balok A bermassa 1 kg berada di atas lantai licin dan balok B bermassa 2 kg digantung seperti gambar. Kedua balok mula-mula diam kemudian bergerak sehingga balok B menyentuh lantai. Berapa waktu yang diperlukan balok B sampai menyentuh lantai?
$W_{A}^{'}=m_{A}.g\sin 30\\W_{A}^{'}=10.10.0,5=50N\\W_{B}=m_{B}.g\\W_{B}=20.10=200N$
Karena WB lebih besar dari WA', maka balok B akan bergerak turun dan balok A bergerak naik searah bidang miring
a. percepatan sistem
$a=\frac{W_{B}-W_{A}^{'}}{m_{A}+m_{B}}\\a=\frac{200-50}{10+20}=5ms^{-2}$
b. Gaya tegangan tali
$T = W_{B} -m_{B}.a\\T=200-20(5)\\T = 100 N$
Besar tegangan talinya yaitu T1 = T2 = T = 100 N
Soal dan Penyelesaian Fisika yang anda cari mungkin ada di sini:
3. Balok A bermassa 1 kg berada di atas lantai licin dan balok B bermassa 2 kg digantung seperti gambar. Kedua balok mula-mula diam kemudian bergerak sehingga balok B menyentuh lantai. Berapa waktu yang diperlukan balok B sampai menyentuh lantai?

Penyelesaian Fisika dari Pak Dimpun:
Untuk mengetahui waktu yang dibutuhkan balok B untuk sampai ke lantai maka terlebih dahulu kita harus mengetahui percepatan balok B.
percepatan sistem:
$a=\frac{m_{B}.g}{m_{A}+m_{B}}\\a=\frac{2.10}{1+2}=\frac{20m}{3s}$
waktu balok B untuk sampai ke lantai:
$t=\sqrt{\frac{2h}{a}}=\sqrt{\frac{2.25}{\frac{20}{3}}}\\t=\sqrt{\frac{15}{2}}=\sqrt{7,5}\, s$
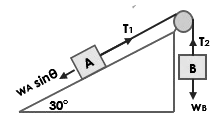
4. Dua balok A dan B dengan massa masing-masing 10 kg dan 20 kg dihubungkan dengan tali melalui katrol seperti gambar. Jika bidang miring tersebut licin.

Untuk mengetahui waktu yang dibutuhkan balok B untuk sampai ke lantai maka terlebih dahulu kita harus mengetahui percepatan balok B.
percepatan sistem:
$a=\frac{m_{B}.g}{m_{A}+m_{B}}\\a=\frac{2.10}{1+2}=\frac{20m}{3s}$
waktu balok B untuk sampai ke lantai:
$t=\sqrt{\frac{2h}{a}}=\sqrt{\frac{2.25}{\frac{20}{3}}}\\t=\sqrt{\frac{15}{2}}=\sqrt{7,5}\, s$
4. Dua balok A dan B dengan massa masing-masing 10 kg dan 20 kg dihubungkan dengan tali melalui katrol seperti gambar. Jika bidang miring tersebut licin.

Hitunglah:
- Percepatan sistem
- Gaya tengangan tali

$W_{A}^{'}=m_{A}.g\sin 30\\W_{A}^{'}=10.10.0,5=50N\\W_{B}=m_{B}.g\\W_{B}=20.10=200N$
Karena WB lebih besar dari WA', maka balok B akan bergerak turun dan balok A bergerak naik searah bidang miring
a. percepatan sistem
$a=\frac{W_{B}-W_{A}^{'}}{m_{A}+m_{B}}\\a=\frac{200-50}{10+20}=5ms^{-2}$
b. Gaya tegangan tali
$T = W_{B} -m_{B}.a\\T=200-20(5)\\T = 100 N$
Besar tegangan talinya yaitu T1 = T2 = T = 100 N
Soal dan Penyelesaian Fisika yang anda cari mungkin ada di sini: