Medan Listrik dan Potensial Listrik Konduktor Keping Sejajar
Soal 1 Sebuah keping dengan luas 0,10 m2 yang dibumikan membawa muatan –8,85 nC ketika diletakkan sejauh 2,0 mm dari sebuah keping identik bermuatan +8,85 nC. Hitung besar kuat medan listrik di antara keping.
Penyelesaian Fisika:
Gaya Listrik:
Soal 1 Sebuah keping dengan luas 0,10 m2 yang dibumikan membawa muatan –8,85 nC ketika diletakkan sejauh 2,0 mm dari sebuah keping identik bermuatan +8,85 nC. Hitung besar kuat medan listrik di antara keping.
Penyelesaian Fisika:
kuat medan listrik:
$\begin{align*} E& = \frac{\sigma }{\varepsilon _o}=\frac{Q}{\varepsilon _oA}\\&= \frac{8,85 \times 10^{-9}}{8,85 \times 10^{-12}} = 10^4 \textrm{N/C}\end{align*}$
Soal 2 Dua keping logam yang sejajar dan jaraknya 0,5 cm satu sam alain diberi muatan listrik yang berlawanan (lihat gambar) hingga memiliki beda potensial 104V. Berapa gaya yang dialami sebauh elektron yang diletakkan di antara kedua keping?
$\begin{align*} E& = \frac{\sigma }{\varepsilon _o}=\frac{Q}{\varepsilon _oA}\\&= \frac{8,85 \times 10^{-9}}{8,85 \times 10^{-12}} = 10^4 \textrm{N/C}\end{align*}$
Soal 2 Dua keping logam yang sejajar dan jaraknya 0,5 cm satu sam alain diberi muatan listrik yang berlawanan (lihat gambar) hingga memiliki beda potensial 104V. Berapa gaya yang dialami sebauh elektron yang diletakkan di antara kedua keping?
Penyelesaian Fisika:
Kuat medan listrik:
$\begin{align*} E &= \frac{V}{d} \\&=\frac{10^4}{5 \times 10^{-3}} \\&= 2 \times 10^6 J\textrm{N/C}\end{align*}$
Gaya listrik yang dialami elektron F:
$\begin{align*} F &= qE \\&= (1,6 x 10^{-19})( 2 x 10^6 ) \\&= 3,2 \times 10^{-13} N\end{align*}$
Soal 3 Sebuah elektron diletakkan di pusat sebuah keping logam bermuatan negatif dan dipercepat menuju keping logam positif didekatnya dengan percepatan sebesar 2x1015 m/s2. Jika kedua keping memiliki rapat muatan yang sama, berapakah nilai rapat muatan ini? (elektron: massa 9x10-31 kg, muatan 1,6x10-19C) dan εo=8,85x10-12 C2/Nm2.
Soal 3 Sebuah elektron diletakkan di pusat sebuah keping logam bermuatan negatif dan dipercepat menuju keping logam positif didekatnya dengan percepatan sebesar 2x1015 m/s2. Jika kedua keping memiliki rapat muatan yang sama, berapakah nilai rapat muatan ini? (elektron: massa 9x10-31 kg, muatan 1,6x10-19C) dan εo=8,85x10-12 C2/Nm2.
Penyelesaian Fisika:
Hukum Newton:
$\begin{align*}F&=ma\\ &=( 9\times 10^{-31})( 2,0 \times 10^{15})\\&=18,0\times 10^{-16}N\end{align*}$ Hukum Newton:
$\begin{align*}F_L &= qE\\&= q(\frac{\sigma }{\varepsilon _o}) \\ & = 1,6\times 10^{-19}\frac{\sigma }{ 8,85\times 10^{-12}}\\&=1,8.10^{-8}\sigma N\end{align*}$
Gaya Listrik = gaya Newton:
$\begin{align*}F_L&=F\\ 18,2\times 10^{-16}&=1,8.10^{-8}\sigma \\\sigma&=\frac{ 18,2\times 10^{-16}}{1,8\times 10^{-8}}\\&=10^{-7}\textrm{C.m}^{-2}\\&=0,1\mu\textrm{C.m}^{-2} \end{align*}$
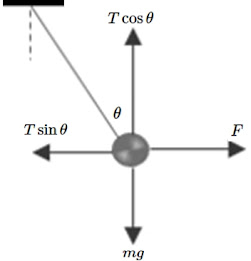
Soal 4 Sebuah partike bermuatan q dan bermassa m digantung dengan seutas kawat dan diletakkan di ruang antara dua keping sejajar yang diberi muatan samatetapi berbeda jenis dengan rapat muatan σ. Pada saat keseimbangan, kawat membentuk sudut θ terhadap arah vertikal (lihat gambar).
Soal 4 Sebuah partike bermuatan q dan bermassa m digantung dengan seutas kawat dan diletakkan di ruang antara dua keping sejajar yang diberi muatan samatetapi berbeda jenis dengan rapat muatan σ. Pada saat keseimbangan, kawat membentuk sudut θ terhadap arah vertikal (lihat gambar).
Tentukan nilai tan θ!
Penyelesaian Fisika:
Kita uraikan gaya-gaya yang bekerja pada muatan q:
Penyelesaian Fisika:
Kita uraikan gaya-gaya yang bekerja pada muatan q:
$\begin{align*}\textrm{sumbu x: }\Sigma F_x &= 0 \\ T\sin \theta &= F\\T\sin \theta & = \frac{q\sigma }{\varepsilon _o}...(1)\\\textrm{sumbu y: }\Sigma F_y &= 0 \\T \cos \theta &=mg...(2)\\ \textrm{Pers (1)}&\textrm{ bagi pers (2):}&\\(1)...T\sin \theta &= \frac{q\sigma }{\varepsilon _o}\\(2)...T \cos \theta &=mg\\\hline \tan \theta&=\frac{q\sigma }{mg\varepsilon _o} \end{align*}$
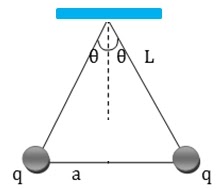
Soal 5 Dua buah bola identik bermuatan memiliki massa 3,0 x 102 kg digantung seperti seperti pada gambar.
Soal 5 Dua buah bola identik bermuatan memiliki massa 3,0 x 102 kg digantung seperti seperti pada gambar.
Panjang L setiap tali adalah 0,15m. Massa tali dan hambatan udara diabaikan. Bila tan θ = 0,0875, sin θ = 0,0872 dan g = 10m/s2 maka besar muatan pada setiap bola adalah ….
Penyelesaian Fisika:
Jarak kedua muatan;
$\begin{align*}\sin\theta&=\frac {\frac{1}{2}r}{L}\\r&=2L\sin\theta \\&=2(0,15)0,0872\\&=0,02616m\end{align*}$
$\begin{align*}\textrm{sumbu x: }\Sigma F_x &= 0 \\ T\sin \theta = F=&\frac{kq^2}{r^2}...(1)\\\textrm{sumbu y: }\Sigma F_y &= 0 \\T \cos \theta =mg&.....(2)\\ \textrm{Pers (1)}&\textrm{ bagi pers (2):}&\\(1)...T\sin \theta = &\frac{kq^2}{r^2}\\(2)...T \cos \theta =&mg\\\hline \tan \theta=&\frac{kq^2 }{mgr^2} \\q=r&\sqrt{\frac{mg\tan\theta}{k}}\\=0,02616 &\sqrt{\frac{300(10)(0,0875)}{9.10^9}}\\=4,4\times 1&0^{-8}C=44nC\end{align*}$
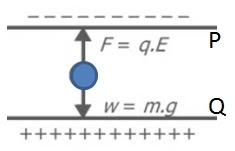
Soal 6 Sebuah bola kecil bermuatan listrik 10 μC berada dalam keadaan seimbang di antara keping sejajar P dan Q dengan muatan yang berbeda jenis dengan rapat muatan 1,77 × 10-8 C/m2.
Soal 6 Sebuah bola kecil bermuatan listrik 10 μC berada dalam keadaan seimbang di antara keping sejajar P dan Q dengan muatan yang berbeda jenis dengan rapat muatan 1,77 × 10-8 C/m2.
Jika g = 10 m/s2 dan permitivitas udara adalah 8,85 × 10-12 C2/Nm2, hitung massa bola tersebut!
Penyelesaian Fisika:
$\begin{align*} E& = \frac{\sigma }{\varepsilon _o}\\&= \frac{1,77\times 10^{-8}}{8,85 \times 10^{-12}} \\&=2. 10^3 \textrm{N/C}\end{align*}$
$\begin{align*} E& = \frac{\sigma }{\varepsilon _o}\\&= \frac{1,77\times 10^{-8}}{8,85 \times 10^{-12}} \\&=2. 10^3 \textrm{N/C}\end{align*}$
Muatan seimbang:
$\begin{align*}F&=W\\qE&=mg\\m&=\frac{qE}{g}\\&=\frac{10. 10^{-6}(2.10^3)}{10}\\&=2.10^{-3}\textrm{kg}=2\textrm{gram}\end{align*}$
