Begini Pertanyaannya...
Tentukan titik berat bidang di bawah ini...
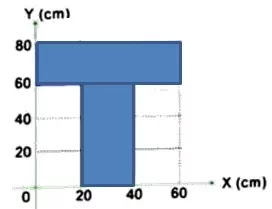
Masih ingat Langkah mudah menghitung koordinat titik berat benda ala Pak Dimpun? baik kita tulis ulang:
- Bagi benda, menjadi beberapa bagian sederhana.
- Hitung (tergantung bentuk benda) masing-masing bagian.
- panjang (garis - satu dimensi) :$ L_1, L_2, dst$
- luas (luasan - dua dimensi) :$A_1, A_2, dst$
- volume (tiga dimensi):$V_1, V_2, dst$
- massa, berat, dll (benda titik) :$ m_1, m_2, dst$
- Tentukan koordinat titik berat masing-masing bagian (X, Y ):
$\begin{align*} &(X_1,Y_1)\\&(X_2,Y_2)\\&dst...\end{align*}$ - Hitung Xo dan Yo : Misalkan benda berbentuk garis, maka yang kita hitung adalah panjang, persamaan menjadi:
$\small\begin{align*}X_o&=\frac {L_1X_1+L_2X_2+...}{L_1+L_2+...} \\Y_o&=\frac {L_1Y_1+L_2Y_2+...}{L_1+L_2+...}\end{align*}$ - Tuliskan koordinat titik berat benda;
$\begin{align*} Z_o&=(X_o;Y_o)\end{align*}$
Kita ikuti Langkah mudah ala Pak Dimpun:
- Kita bagi benda, dalam hal ini kita bagi menjadi 2 bagian, satu persegi panjang bawah yang vertikal dan satu persegi panjang atas yang horizontal.
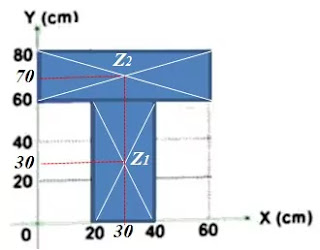
- Kita hitung Luas masing-masing bagian:
$\begin{align*} A_1&=20\times 60=1200\\A_2&=20\times 60=1200\end{align*}$ - Kita tentukan koordinat titik berat masing-masing bagian, untuk benda homogen titik berat persis di tengah.
$\begin{align*} X_1&=20+\frac{1}{2}(20)\\&=30\\Y_1&=\frac{1}{2}(60)\\&=30\\X_2&=\frac{1}{2}(60)\\&=30\\Y_2&=60+\frac{1}{2}(20)\\&=70\end{align*}$ - Kita hitung Xo dan Yo:
$\small \begin{align*}X_o&=\frac {A_1X_1+A_2X_2}{A_1+A_2} \\&=\frac {1200(30)+1200(30)}{1200+1200}\\X_o&=30\\\\Y_o&=\frac {A_1Y_1+A_2Y_2}{A_1+A_2} \\&=\frac {1200(30)+1200(70)}{1200+1200}\\Y_o&=50 \end{align*}$ - Kita tuliskan koordinat titik berat benda;
$\begin{align*} Z_o&=(30,50)\end{align*}$cm







