Soal dan Penyelesaian Fisika SMA - Soal dan Pembahasan Kesetimbangan benda tegar. Kesetimbangan benda tegar adalah kondisi dimana suatu benda berada dalam kesetimbangan rotasi (artinya benda tersebut tidak mengalami rotasi / pergerakan).
Benda tegar adalah istilah yang sering digunakan dalam dunia Fisika untuk menyatakan suatu benda yang tidak akan berubah bentuknya setelah diberikan suatu gaya pada benda itu.
Banyak yang mengatakan, soal kesetimbangan benda tegar adalah bagian tersulit dalam fisika, karena pada soal kesetimbangan benda tegar, beda gambar soal, beda cara menyelesaikannya.
Itu adalah anggapan yang tidak tepat, karena konsep kesetimbangan benda tegar hanya mengikuti dua syarat, antara lain:
1. Resultan gaya terhadap suatu titik sembarang sama dengan nol.\begin{align*} \Sigma F=0\end{align*}
2. Resultan momen gaya harus bernilai nol \begin{align*} \Sigma \tau =0\end{align*}
SOAL DAN PENYELESAIAN KESETIMBANGAN BENDA TEGAR
1.Sebuah balok bermassa 5 kg diletakkan diatas papan kayu yang bermassa 10 kg. Papan tersebut bertumpu pada kaki A dan C. Jika jarak beban dari kaki A sejauh 1 m dan panjang papan kayu 5 m, maka hitunglah gaya yang dialami oleh kaki A!
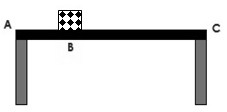
Penyelesaian Soal Kesetimbangan:
Perhatikan gambar di berikut ini...
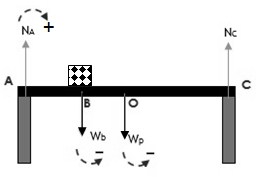
Gaya normal pada kaki A ( NA )
Dengan kesepakatan: searah jarum jam POSITIP dan belawanan arah jarum jam NEGATIP, maka:$\begin{align*} \Sigma \tau _{C}&=0 \\N_{A}(AC)&=W_{b}(BC)+W_{p}(OC)\\N_{A}5)&=50(4)+100(2,5)\\5N_{A}&=450\\N_{A}&=90N \end{align*} $
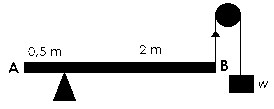
2.Pada gambar berikut batang AB beratnya 100 N.
Dengan kesepakatan: searah jarum jam POSITIP dan belawanan arah jarum jam NEGATIP, maka:$\begin{align*} \Sigma \tau _{C}&=0 \\N_{A}(AC)&=W_{b}(BC)+W_{p}(OC)\\N_{A}5)&=50(4)+100(2,5)\\5N_{A}&=450\\N_{A}&=90N \end{align*} $
2.Pada gambar berikut batang AB beratnya 100 N.

Sistem dalam keadaan seimbang ($\Sigma \tau_{O}=0$ ) maka:
$\begin{align*} \Sigma \tau _{O}&=0\\T(OB)&=W_{t}(OP)\\W(2)&=100(0,75)\\W&=37,5N \end{align*}$
3. Sebuah batang homogen AB dengan panjang 40 cm dan berat 10N. Pada ujung batang digantung beban seberat 20N, batang ditahan oleh tali T sehingga sistem seimbang seperti pada gambar. Jika sudut yang dibentuk oleh tali T dengan batang adalah 37°, maka besar tegangan tali T adalah!

Penyelesaian Soal Kesetimbangan:

3. Sebuah batang homogen AB dengan panjang 40 cm dan berat 10N. Pada ujung batang digantung beban seberat 20N, batang ditahan oleh tali T sehingga sistem seimbang seperti pada gambar. Jika sudut yang dibentuk oleh tali T dengan batang adalah 37°, maka besar tegangan tali T adalah!

Penyelesaian Soal Kesetimbangan:

Sistem dalam keadaan seimbang ($\Sigma \tau_{A}=0$ ) maka:
$\begin{align*} \Sigma \tau _{A}&=0 \\W_{B}(AB)+W_{b}(AO)&=T\sin 37^{o}(AB)\\20(0,4)+10(0,2)&=T(0,6)(0,4)\\T&=41,67N \end{align*}$
Cara WOW dari Pak Dimpun:
$\begin{align*}T&=\frac{W_{Bbn}+\frac{1}{2}W_{btg}}{\sin \theta }\\T&=\frac{20+\frac{1}{2}.10}{\sin 37 }\\T&=\frac{25}{0,75}\\T&=41,67N \end{align*}$
4. Sebuah batang homogen AC dengan panjang panjang 4 m dan massanya 50 kg. Pada ujung C digantungkan beban yang massanya 20 kg. Batang ditahan oleh tali T sehingga sistem seimbang. Jika jarak BC 1 m, maka hitunglah tegangan tali T!

Penyelesaian Soal Kesetimbangan:
Perhatikan gambar:

$\begin{align*} \Sigma \tau _{A}&=0 \\W_{B}(AB)+W_{b}(AO)&=T\sin 37^{o}(AB)\\20(0,4)+10(0,2)&=T(0,6)(0,4)\\T&=41,67N \end{align*}$
Cara WOW dari Pak Dimpun:
$\begin{align*}T&=\frac{W_{Bbn}+\frac{1}{2}W_{btg}}{\sin \theta }\\T&=\frac{20+\frac{1}{2}.10}{\sin 37 }\\T&=\frac{25}{0,75}\\T&=41,67N \end{align*}$
4. Sebuah batang homogen AC dengan panjang panjang 4 m dan massanya 50 kg. Pada ujung C digantungkan beban yang massanya 20 kg. Batang ditahan oleh tali T sehingga sistem seimbang. Jika jarak BC 1 m, maka hitunglah tegangan tali T!

Penyelesaian Soal Kesetimbangan:
Perhatikan gambar:

Sistem dalam keadaan seimbang ($\Sigma \tau_{A}=0$ ) maka:
$\begin{align*} \Sigma \tau _{A}=0 \\W_{B}(AC)+W_{b}(AO)&=T\sin 30^{o}(AB)\\200(4)+500(2)&=T(0,5)(3)\\T&=1200N \end{align*}$
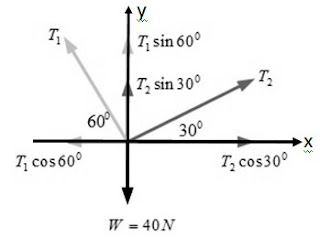
5. Sebuah benda bermassa 4 kg digantung dengan menggunakan tali dengan teknik gantungan seperti pada gambar. Tali pertama dan tali kedua diikatkan pada dinding atas sehinga keadaan benda setimbang, maka besar tegangan tali pertama dan tali kedua adalah..

Penyelesaian Soal Kesetimbangan:
Analisa gaya pada soal sbb:
$\begin{align*} \Sigma \tau _{A}=0 \\W_{B}(AC)+W_{b}(AO)&=T\sin 30^{o}(AB)\\200(4)+500(2)&=T(0,5)(3)\\T&=1200N \end{align*}$
5. Sebuah benda bermassa 4 kg digantung dengan menggunakan tali dengan teknik gantungan seperti pada gambar. Tali pertama dan tali kedua diikatkan pada dinding atas sehinga keadaan benda setimbang, maka besar tegangan tali pertama dan tali kedua adalah..

Penyelesaian Soal Kesetimbangan:
Analisa gaya pada soal sbb:

- Jumlah gaya pada sumbu x = nol: $\Sigma F_x=0:$
- $\begin{align*} T_{1}\cos 60&=T_{2}\cos 30\\T_{1}(0,5)&=T_{2}(0,5\sqrt{3})\\T_{1}&=T_{2}\sqrt{3}.......(1)\end{align*}$
- Jumlah gaya pada sumbu y = nol: $\Sigma F_y=0:$
- $\begin{align*} T_{1}\sin 60+T_{2}\sin 30&=W\\T_{1}(0,5\sqrt{3})+T_{2}(0,5)&=40\\T_{1}(\sqrt{3})+T_{2}&=80.......(2)\end{align*}$
- Substitusi persamaan (1) ke (2) diperoleh:
$\begin{align*} T_{2}\sqrt{3}(\sqrt{3})+T_{2}&=80\\4T_{2}&=80\\ T_{2}&=20N\\T_{1}&=\sqrt{3}T_{2}\\T_{1}&=20\sqrt{3}N \end{align*}$
$\begin{align*} T_{1}&=W\sin 60\\T_{1}&=40(0,5\sqrt{3})\\T_{1}&=20\sqrt{3}N\\T_{2}&=W\sin 30\\T_{2}&=40(0,5)\\T_{2}&=20N\end{align*}$
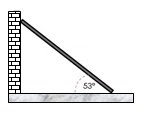
6.Sebuah tangga sepanjang L meter dengan berat 400 N disandarkan pada dinding licin dan lantai kasar seperti gambar. Jika tangga tepat akan tergelincir ketika sudut tangga dengan lantai 53o maka hitunglah koefisien gesekan antara lantai dan tangga!
6.Sebuah tangga sepanjang L meter dengan berat 400 N disandarkan pada dinding licin dan lantai kasar seperti gambar. Jika tangga tepat akan tergelincir ketika sudut tangga dengan lantai 53o maka hitunglah koefisien gesekan antara lantai dan tangga!
Penyelesaian Soal Kesetimbangan:


-
Jumlah gaya pada sumbu x = nol: $\Sigma F_x=0:$
$\begin{align*} \Sigma F_{x}&=0\\N_{B}&=f_{A}=\mu _{A}N_{A}.....(1)\end{align*}$ - Jumlah gaya pada sumbu y &= nol: $\Sigma F_y=0:$
$\begin{align*} N_{B}&=\mu _{A}N_{A}=400\mu _{A} \end{align*}$ - Jumlah torsi di A &= nol: ΣτA &= 0:
$\begin{align*} N_{B}\sin \theta (AB)&=W_{t}\cos \theta (AO)\\400\mu _{A}(0,8) (L)&=400(0,6)(0,5L)\\\mu _{A}&=\frac{3}{8}=0,375 \end{align*}$
$\begin{align*}\mu _{A}&=\frac{1}{2\tan \theta}\\\mu _{A}&=\frac{1}{2\tan 53^{^{0}}}\\\mu _{A}&=\frac{1}{2\cdot \frac{4}{3}}\\\mu _{A}&=\frac{3}{8}\end{align*}$
Yang Anda Cari Mungkin di sini:
Yang Anda Cari Mungkin di sini: