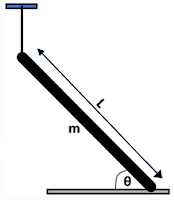
1. Salah satu ujung sebuah tongkat homogen (massa m dan panjang tali L), tergantung dengan menggunakan tali dan ujung tongkat lainnya bersentuhan dengan lantai dalam keadaan diam. Tongkat tersebut membentuk sudut θ terhadap horisontal. Tentukan nilai gaya tegangan tali!
Jawaban Fisika dari Pak Dimpun
Untuk menghitung tegangan tali, pertama-tama kita gambarkan gaya yang bekerja pada benda, lalu kita gunakan syarat keseimbangan.
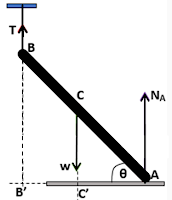
Kita ambil jumlah momen gaya di A sama dengan nol.\[\\\Sigma \tau _{A}= 0\\ W . \frac{1}{2} L \cos \theta = T . L\cos \theta \\ T = \frac{1}{2}W\]
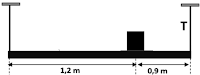
2. Dua kabel digunakan untuk menopang batang horizontal bermassa 9,0 kg yang panjangnya 2,1 m. Pada batang diletakkan sebuah kotak bermassa 21 kg seperti yang ditunjukkan pada gambar di bawah ini! Tentukan tegangan tali T!
Jawaban Fisika dari Pak Dimpun
Ayo kita gambarkan gayanya...
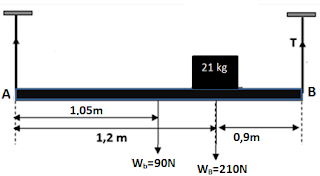
Kita ambil jumlah momen gaya di A sama dengan nol.\[\\\Sigma \tau _{A}=0\\T(2,1) = W_{b}.(1,05)+W_{B}.(1,2)\\T(2,1) = 90.(1,05)+210.(1,2)\\T(2,1) = 346,5 \\T = 165 N\]
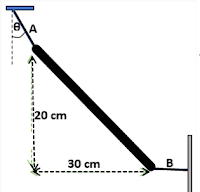
3. Batang homogen bermassa m diikat dengan tali A dan B setimbang pada posisi seperti pada gambar di bawah ini, dengan tali B horisontal. Tentukan nilai tan θ.
 Jawaban Fisika dari Pak Dimpun
Jawaban Fisika dari Pak DimpunAyo kita gambarkan gayanya...

\[\\\Sigma F_{x} = 0\\T_{B} = T_{A}\sin \theta .....(1)\\ \Sigma F_{y} = 0\\W = T_{A}\cos \theta .....(2)\] Substitusi persamaan (1) ke persamaan (2)\[\\\tan \theta =\frac{T_{B}}{W}\\T_{B}=W\tan \theta ...(3)\]Kita ambil jumlah momen gaya di P sama dengan nol.\[\\\Sigma \tau _{P} = 0\\ T_{B}. L \sin \alpha = W . \frac{1}{2} L \cos \alpha \\ T_{B} = \frac{1}{2}W\cot \alpha ....(4)\]Substitusi persamaan (3) ke persamaan (4) diperoleh\[\\W\tan \theta =\frac{1}{2}W\cot \alpha \\\tan \theta =\frac{1}{2}\cot \alpha \\\tan \theta =\frac{1}{2}(\frac{30}{20}) =\frac{3}{4}\]
4. Sebuah balok batang homogen diengsel pada lantai dan berdiri tegak seperti pada sistem gambar di bawah ini. Tentukan besar $T_1,T_2$ dan gaya-gaya yang bekerja pada engsel!

Jawaban Fisika dari Pak Dimpun
Gaya-gaya bebas yang bekerja pada benda ditunjukkan pada gambar di bawah ini,
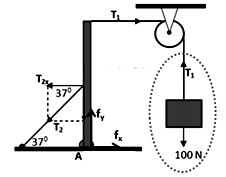
Berat beban 100 N, kita peroleh
\[T_1=100N\]Kita ambil jumlah momen gaya di A sama dengan nol.\[\\\Sigma \tau _{A}=0\\ T_{2} \cos 37(\frac{1}{2}L) = T_{1}(L)\\T_{2} (\frac{4}{5})(\frac{1}{2}) = 100\\T_{2} = 250 N\]Jumlah gaya-gaya pada sumbu x sama dengan nol\[\\\Sigma F_{x} = 0\\T_{2x}=T_{1} + f_{x}\\f_{x} = T_{2x} - T_{1}\\f_{x} = T_2 \cos 37-T_{1}\\f_x = 250(\frac{4}{5})-100\\f_x = 100 N\]Jumlah gaya-gaya pada sumbu y sama dengan nol\[\\\Sigma F_{y} = 0\\f_{y}=T_{2y}\\ f_y = T_2 \sin 37=250(\frac{3}{5})\\ Fy = 150 N\]baca juga:







