Itu adalah anggapan yang tidak tepat, karena konsep benda tegar hanya mengikuti dua syarat, antara lain:
- Resultan gaya terhadap suatu titik sembarang sama dengan nol.\[\Sigma F=0\]
- Resultan momen gaya harus bernilai nol\[\Sigma \tau =0\]
SOAL DAN PENYELESAIAN KESETIMBANGAN DAN TITIK BERAT
Soal 1. Bila diketahui sistem berikut ini berada dalam keadaan setimbang.
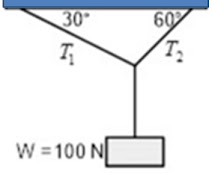
Tentukanlah besar gaya tegang tali T1dan T2.
A. T1 = 50N dan T2=50N
B. T1 = 50N dan T2=50$\small \sqrt{3}$ N
C. T1 = 50$\small \sqrt{3}$ N dan T2=50$\small \sqrt{3}$ N
D. T1 = 50$\small \sqrt{2}$ N dan T2=50$\small \sqrt{3}$ N
E. T1 = 50N dan T2=50N
Cara WOW dari Pak Dimpun
Perhatikan gambar:
$T_{1}=W\sin 30^{o}\\T_{1}=100.(0,5)=50N$
$T_{2}=W\sin 60^{o}\\T_{2}=100.(0,5 \sqrt{3})=50 \sqrt{3}N$
Soal 2. Batang AB homogen dengan berat 40 N digantung dengan dua utas tali (massa diabaikan ) yang masing – masing berkekuatan 50N dan 100 N (gambar).
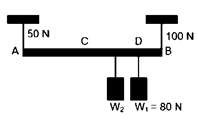
Apabila kedua tali hampir putus, sedangkan AC = CB = 4m dan DB=1m. Tentukan letak W2 terhadap titik C !
$T_{2}=W\sin 60^{o}\\T_{2}=100.(0,5 \sqrt{3})=50 \sqrt{3}N$
Soal 2. Batang AB homogen dengan berat 40 N digantung dengan dua utas tali (massa diabaikan ) yang masing – masing berkekuatan 50N dan 100 N (gambar).

Apabila kedua tali hampir putus, sedangkan AC = CB = 4m dan DB=1m. Tentukan letak W2 terhadap titik C !
A. 4/3 m di kanan C
B. 4/3 m di kiri C
C. 2/3 m di kanan C
D. 0,8 m di kiri C
E. 0,8 m di kiri C
Penyelesaian Kesetimbangan:
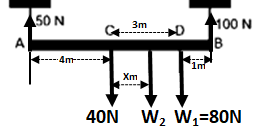
Kita gambar seluruh gaya yang bekerja pada sistem: Kita hitung besar nilai W2:
B. 4/3 m di kiri C
C. 2/3 m di kanan C
D. 0,8 m di kiri C
E. 0,8 m di kiri C
Penyelesaian Kesetimbangan:

Kita gambar seluruh gaya yang bekerja pada sistem: Kita hitung besar nilai W2:
$\Sigma F _{y}=0\\F_{A}+F_{B}=W_{B}+W_{1}+W_{2}\\50+100=40+W_{2}+80\\W_{2}=30N$
Kita ambil Jumlah momen gaya di C = 0:$\small \\\Sigma \tau _{C}=0\\T_{A}(AC)+W_{2}(x)+W_{1}(CD)=T_{B}(BC)\\50(4)+30(x)+80(3)=100(4)\\x=-\frac{4}{3}m\\x=\frac{4}{3}m\; di\; kiri\; C$
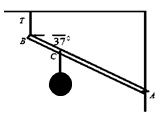
Soal 3. Batang AB memiliki massa 5kg digantungi beban P bermassa 2kg.
Soal 3. Batang AB memiliki massa 5kg digantungi beban P bermassa 2kg.
Jika BC = ¼AB. Tentukan besar tegangan tali T !
A. 35 N
A. 35 N
B. 25 N
C. 40 N
D. 45 N
E. 50 N
Penyelesaian Kesetimbangan:
Kita gambarkan gaya pada sistem

Kita gunakan syarat keseimbangan:
C. 40 N
D. 45 N
E. 50 N
Penyelesaian Kesetimbangan:
Kita gambarkan gaya pada sistem

Kita gunakan syarat keseimbangan:
$\Sigma \tau _{A}=0\\W(\frac{1}{2}L\cos 37)+W_{b}(\frac{3}{4}L\cos 37)=T(L\cos 37)\\W(\frac{1}{2})+W_{b}(\frac{3}{4})=T\\T=50(\frac{1}{2})+20(\frac{3}{4})\\T=40N$
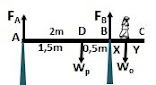
Soal 4. Batang AC bermassa 40 kg dan panjangnya 3 m. Jarak tumpuan A dan B adalah 2 m (di B papan dapat berputar). Seorang anak (massa 30 kg) berjalan dari A menuju ke C.
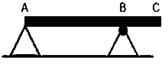
Berapa jarak minimum anak dari titik C agar papan tetap seimbang (ujung batang A hampir terangkat ke atas)
A. 1/3 m
B. 2/5 m
C. 3/5 m
D. ¾ m
E. 0,4m
Penyelesaian Kesetimbangan:
Kita gambarkan gaya pada sistemGunakan syarat keseimbangan,
$\Sigma \tau _{B}=0\\W_{b}(0,5)=W_{o}(x)\\400(0,5)=300(x)\\\\ x=\frac{2}{3}m\\y=1=x\\y=1-\frac{2}{3}\\y=\frac{1}{3}m$
lanjut ke Soal Titik berat....
Soal 4. Batang AC bermassa 40 kg dan panjangnya 3 m. Jarak tumpuan A dan B adalah 2 m (di B papan dapat berputar). Seorang anak (massa 30 kg) berjalan dari A menuju ke C.
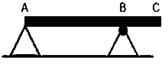
Berapa jarak minimum anak dari titik C agar papan tetap seimbang (ujung batang A hampir terangkat ke atas)
A. 1/3 m
B. 2/5 m
C. 3/5 m
D. ¾ m
E. 0,4m
Penyelesaian Kesetimbangan:
Kita gambarkan gaya pada sistemGunakan syarat keseimbangan,
$\Sigma \tau _{B}=0\\W_{b}(0,5)=W_{o}(x)\\400(0,5)=300(x)\\\\ x=\frac{2}{3}m\\y=1=x\\y=1-\frac{2}{3}\\y=\frac{1}{3}m$
lanjut ke Soal Titik berat....