1. Setelah meluruh selama 30 jam, suatu unsur radioaktif tinggal 25 % dari jumlah semula. tentukan :
a.Waktu paruh unsur radioaktif tersebut;
b.Jumlah radio aktif yang tersisa setelah 60 jam !
Jawaban Fisika Pak Dimpun
a. Waktu paruh;
\[ \\N=N_o{\left( \frac{1}{2} \right)}^{\frac{t}T_{\frac{1}{2}}}\\ 25\%N_o=N_o{\left( \frac{1}{2} \right)}^{\frac{30}{T_{1/2}}}\\ \\\frac{1}{4}={\left( \frac{1}{2} \right)}^{\frac{30}{T_{1/2}}}\\ \\\left ( \frac{1}{2} \right )^2=\left ( \frac{1}{2} \right )^{\frac{30}{T_{\frac{1}{2}}}}\\2={\frac{30}{T_{\frac{1}{2}}}}\\T_{\frac{1}{2}}=\frac{30}{2}=15jam\]
b. Jumlah yang tersisa setelah 60 jam
\[ \\N=N_o{\left( \frac{1}{2} \right)}^{\frac{t}{T_{1/2}}} \\N=N_o{\left( \frac{1}{2} \right)}^{\frac{60}{15}} \\N=N_o{\left( \frac{1}{2} \right)}^{4} \\N=\left( \frac{1}{16} \right)N_o\\N=6,25\%N_o\]
2. Perhatikan gambar
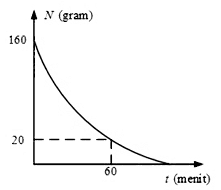
Sebuah radioaktif mengalami peluruhan yang digambarkan grafik peluruhan massanya terhadap waktu seperti pada gambar di atas. Tentukan :
a. Besar waktu paruh;
b. Ketetapan peluruhan;
c. Waktu yang dibutuhkan supaya bahan radioaktif tersebut tinggal 10% !
Jawaban Fisika Pak Dimpun
a. Waktu paruh
\[ \\N=N_o\left( \frac{1}{2} \right)^{\frac{t}{T_{\frac{1}{2}}}}\\ \frac{20}{160}=\left( \frac{1}{2} \right)^{\frac{t}{T_{\frac{1}{2}}}}\\ \frac{1}{8}=\left( \frac{1}{2} \right)^{\frac{60}{T_{\frac{1}{2}}}}\\ 3=\frac{60}{T_{\frac{1}{2}}}\\ {T_{\frac{1}{2}}}=20\text{ menit}\] b. Konstanta peluruhan
\[ \\T_{\frac{1}{2}}=\frac{\ln 2}{\lambda }\\ \lambda =\frac{\ln 2}{{T_{\frac{1}{2}}}}\\ \lambda =\frac{0,693}{20}\\ \lambda \approx 0,035\text{ meni}{{\text{t}}^{-1}}\] c. Waktu supaya tinggal 10% dari bahan semula
\[ \\N=N_o{\left( \frac{1}{2} \right)}^{\frac{t}{T_{1/2}}}\\ \frac{N}{N_o}={\left( \frac{1}{2} \right)}^{\frac{t}{T_{1/2}}}\\ \frac{1}{10}={\left( \frac{1}{2} \right)}^{\frac{t}{20}}\\ \log 10=\frac{t}{20}\log 2\\ 1=\frac{t}{20}(0,3)\\ t=\frac{20}{0,3}\\ t=66,7\text{ menit}\]
3. Isotop bismuth memiliki waktu paruh 60,5 detik Tentukan :
a. Konstanta peluruhan;
b. Banyaknya isotop bismuth yang tersisa dalam waktu 121 detik, jika pada keadaan awal terdapat 1000 gram bismuth 212 !
Jawaban Fisika Pak Dimpun
a. Konatanta peluruhan
\[ \\\lambda =\frac{\ln 2}{{{T}_{1/2}}}\\ \lambda =\frac{0,693}{60,5}=0,0115\text{ deti}{{\text{k}}^{-1}}\] b. isotop yang tersisa dalam waktu 121 detik
\[ \\N=N_o\left( \frac{1}{2} \right)^{\frac{t}{T_{1/2}}}\\ N=1000{\left( \frac{1}{2} \right)}^{\frac{121}{60,5}}\\ N=1000{\left( \frac{1}{2} \right)}^{2}\\ N=1000\left( \frac{1}{4} \right)=250\text{ gram}\]
4. Sebuah benda dari kayu tua memiliki 20% karbon radioaktif dibandingkan dengan kayu segar. Berapa umur kayu tua tersebut jika waktu paruh karbon radioaktif tersebut 5700 tahun ?
Jawaban Fisika Pak Dimpun
\[ \\N=N_o{{\left( \frac{1}{2} \right)}^{\frac{t}{T_{1/2}}}} \\\frac{N}{N_o}={{\left( \frac{1}{2} \right)}^{\frac{t}{T_{1/2}}}} \\\frac{2}{10}={{\left( \frac{1}{2} \right)}^{\frac{t}{5700}}} \\log\frac{1}{5}=log{{\left( \frac{1}{2} \right)}^{\frac{t}{5700}}} \\\log 5=\frac{t}{5700}\log 2 \\t=\frac{5700\log 5}{\log 2} \\t=5700(2.32)\\t=13.235\]
5. Jika Tetapan atau konstanta peluruhan zat radioaktif adalah 6,93 x10-5 Bq. Setelah 200 detik aktivitas pancarannya menjadi 4 x 106 Bq. Hitunglah aktivitasa wal atau mula mula zat radioaktif tersebut.
Jawaban Fisika Pak Dimpun:
\[ \\T_{\frac{1}{2}}=\frac{\ln 2}{\lambda }\\T_{\frac{1}{2}}=\frac{0,693}{6,93 x10^{-5} }\\T_{\frac{1}{2}}=100s\] \[ \\R=R_o{{\left( \frac{1}{2} \right)}^{\frac{t}{{{T}_{1/2}}}}}\\4 x 10^6=R_o{\left( \frac{1}{2} \right)}^{\frac{200}{100}}\\R_o=16\times 10^6\\R_o=1,6\times 10^7Bq\]







