Begini pertanyaannya.
Soal 1. Empat buah kapasitor dirangkai seperti pada gambar di bawah.
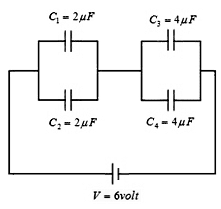tentukanlah BESAR:a. Kapasitas pengganti;
b. Beda potensial masing-masing kapsitor;
c. Muatan pada masing-masing kapasitor;
d. Energi total pada rangkaian !
e. Energi pada masing-masing kapasitor;
Jawaban Fisika Pak Dimpun:
a. Kapasitas pengganti
$C_1$ paralel dengan $C_2$, maka:\begin{align*} C_{12}&=C_1+C_2\\C_{12}&=2+2=4\mu \text{F}\end{align*}$C_3$ paralel dengan $C_4$, maka:\begin{align*} C_{34}&=C_3+C_4\\C_{34}&=4+4=8\mu \text{F}\end{align*}Susunan kapasitor sekarang kita sederhanakan menjadi:
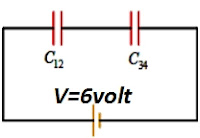
$C_{12}$ paralel dengan $C_{34}$, maka: \begin{align*} \frac{1}{C_{tot}}&=\frac{1}{C_{12}}+\frac{1}{C_{34}}\\\frac{1}{C_{tot}}&=\frac{1}{4}+\frac{1}{8}\\\frac{1}{C_{tot}}&=\frac{2+1}{8}\\C_{tot}&=\frac{8}{3}\mu \text{F}\end{align*}b. Beda potensial pada masing-masing kapsitor;
Muatan total rangkaian:\begin{align*}Q_{tot}&= Q_{12}=Q_{34}\\Q_{tot}&=C_{tot}{V_{tot}}\\Q_{tot}&=\frac{8}{3}(6)=16\mu \text{F}\end{align*}Beda potensial $C_{12}$:\begin{align*}V_{12}=\frac{Q_{12}}{C_{12}}=\frac{16}{4}=4\text{ V}\end{align*}Karena $C_{12}$ paralel dengan $C_{34}$, maka: \begin{align*}V_{12}=V_1=V_2=4\text{ V}\end{align*}Beda potensial $C_{34}$:\begin{align*}V_{34}=\frac{Q_{34}}{C_{34}}=\frac{16}{8}=2\text{ V}\end{align*}Karena $C_{3}$ paralel dengan $C_{4}$, maka: \begin{align*}V_{34}=V_3=V_4=2\text{ V}\end{align*}c. Muatan pada masing-masing kapasitor: \begin{align*}Q_{1}&={{V}_{1}}{{C}_{1}}=4\times 2=8\text{ }\mu C\\Q_{2}&={{V}_{2}}{{C}_{2}}=4\times 2=8\text{ }\mu C\\Q_{3}&={{V}_{3}}{{C}_{3}}=2\times 4=8\text{ }\mu \text{C}\\Q_{4}&={{V}_{4}}{{C}_{4}}=2\times 4=8\mu C\end{align*}d. Besar energi total pada rangkaian !: \begin{align*}E&=\frac{1}{2}{C_t}V_t^2=\frac{1}{2}(\frac{8}{3}){{\left( 6 \right)}^{2}}=48\text{ }\mu \text{J}\end{align*}e. Besar energi masing-masing kapasitor:\begin{align*}E_1&=\frac{1}{2}{C_1}V_1^2=\frac{1}{2}2{{\left( 4 \right)}^{2}}=16\text{ }\mu \text{J}\\E_2&=\frac{1}{2}{C_2}V_2^2=\frac{1}{2}(2){{\left( 4 \right)}^{2}}=16\text{ }\mu \text{J}\\E_3&=\frac{1}{2}{C_3}V_3^2=\frac{1}{2}(4){{\left( 2 \right)}^{2}}=8\text{ }\mu \text{J}\\E_4&=\frac{1}{2}{C_4}V_4^2=\frac{1}{2}(4){{\left( 2 \right)}^{2}}=8\mu \text{J}\end{align*}
Soal 2. Sebuah kapasitor keping sejajar yang luasnya $10cm^2$ dipasang pada beda potensial 12 V, diketahui jarak antar keping 1 mm. Tentukan besar:
a. medan listrik antara dua keping;
b. Rapat muatan pada keping kapasitor
c. Muatan pada keping kapasitor
Jawaban Fisika Pak Dimpun:
a. Medan listrik di dalam kapasitor
\begin{align*} E&=\frac{V}{d}=\frac{12}{{{10}^{-3}}}=1200\text{ N/C}\end{align*} b. Rapat muatan pada keping kapasitor\begin{align*} \sigma &=E{{\varepsilon }_{o}}\\\sigma &=12000\times 8,85\times {{10}^{-12}}\\ \sigma &=1,062\times {{10}^{-7}}\text{ C/}{{\text{m}}^{2}}\end{align*} c. Muatan pada keping kapasitor:\begin{align*} \sigma &=\frac{Q}{A}\\Q&=\sigma A=1,062\times {{10}^{-7}}\times {{10}^{-3}}\\Q&=1,062\times {{10}^{-11}}\text{ C}\end{align*}Baca juga:
