Soal nomor 4. Panjang batang AB adalah 6m, bertumpu pada dinding licin di C, dan panjang BC adalah 1m. Jarak titik A ke dinding yaitu OA adalah 3m. Jika berat batang AB adalah 10Nm, tentukanlah:
a. Koefisien gesek batang dan alasnyab.Gaya normal di titik C
Penyelesaian Fisika:
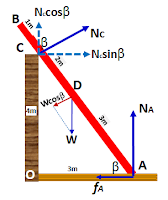Dari gambar diperoleh: \begin{align*} \sin \beta &=\frac{4}{5}=0,8\\\cos \beta &=\frac{3}{5}=0,6\end{align*}Komponen sumbu - x: \begin{align*} \Sigma F_x&=0\\f_A&=N_c\sin \beta \\\mu N_A&=N_c(0,8)\\\mu N_A&=0,8N_c\\N_A&=\frac{0,8 N_c}{\mu }....(1)\end{align*}\begin{align*} \Sigma F_y&=0\\N_c\cos \beta +N_A&=W\\N_c(0,6) +N_A&=W\\N_c(0,6) +N_A&=W...(2)\end{align*}Gantikan nilai NA dari persamaan (1) ke persamaan (2): \begin{align*} N_c( 0,6) +N_A&=W\\0,6N_c+\frac{0,8 N_c}{\mu }&=W\\N_c(0,6+\frac{0,8 }{\mu })&=W\\N_c=\frac{W}{(0,6+\frac{0,8 }{\mu })}&...(3)\end{align*}Ambil jumlah momen gaya di A = 0:\begin{align*} N_c(AC)&=W\cos \beta (AD)\\\frac{W}{(0,6+\frac{0,8 }{\mu })}(5)&=W(0,6)(3)\\\frac{5}{(0,6+\frac{0,8 }{\mu })}&=1,8\\1,08+\frac{1,44 }{\mu }&=5\\\frac{1,44 }{\mu }&=3,92\\\mu&=\frac{1,44}{3,93}\approx 0,37\end{align*}Koefisien gesekan antara batang dengan lantai di titik A sebesar 0,54.Gaya Nornal di C kita ambil dari persamaan (3):\begin{align*} N_c=\frac{W}{(0,6+\frac{0,8 }{\mu })}\\N_c=\frac{6(10)}{(0,6+\frac{0,8 }{0,37})}\\N_c=\frac{60}{2,78}\\N_c=21,58N\end{align*}Kembali ke
