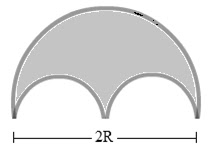
Uji kompetensi 1.5 nomor 1. Jika sebuah pelat dibentuk menjadi seperti terlihat di bawah ini, tentukanlah titik berat pelat tersebut.
Penyelesaian Fisika:
Sebenarnya soal ini sudah kita jawab pada soal nomor 4 post berjudul SOAL DAN PENYELESAIAN TITIK BERAT DAN PUSAT MASSA , namun demikian kita tuliskan lagi di sini.Mari kita ikuti langkah ala Pak Dimpun:
a. Kita bagi benda, menjadi TIGA; Anggap setengah lingkaran besar (berjari-jari R) adalah utuh lalu dikurangi dua buah setengah lingkaran kecil (berjari-jari 0,5R).
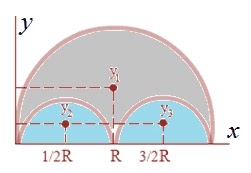
b. Kita hitung luas masing-masing;
\begin{align*}A_1&=\frac{1}{2}\pi R^{2}\\A_2&=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\\A_3&=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\end{align*}c. Kita cari koordinat titik berat masing-masing; \begin{align*}X_1&=R;\\ Y_1&=\frac{4R}{3\pi}\\X_2&=\frac{1}{2} R\\Y_2&=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\\X_3&=\frac{3}{2} R\\Y_3&=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\end{align*}d. Hitung Xo dan Yo,
Untuk sumbu x atau $X_o$;\[\small \begin{align*}X_o&=\frac{A_1.X_1+A_2.X_2+A_3.X_3}{A_1+A_2+A_3} \\X_o&=\frac{\frac{1}{2}\pi R^2(R) -\frac{1}{8}\pi R^2(\frac{R}{2})-\frac{1}{8}\pi R^2(\frac{3R}{2 })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\X_o&=\frac{4(R) -(\frac{R}{2 })-(\frac{3R}{2 })}{2}=\frac{4R}{4}\\X_o&=R\end{align*}\]
Untuk sumbu y atau $Y_o$;\[\small \begin{align*}Y_o&=\frac{A_1.Y_1+A_2.Y_2+A_3.Y_3}{A_1+A_2+A_3} \\Y_o&=\frac{\frac{1}{2}\pi R^2(\frac{4R}{3\pi }) -\frac{1}{8}\pi R^2(\frac{2R}{3\pi })-\frac{1}{8}\pi R^2(\frac{2R}{3\pi })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\Y_o&=\frac{4(\frac{4R}{3\pi }) -(\frac{2R}{3\pi })-(\frac{2R}{3\pi })}{2}=\frac{12R}{6\pi}\\Y_o&=\frac{2R}{\pi}\end{align*}\]e. Tuliskan titik berat;\begin{align*}Z&=(R;\frac{2R}{\pi})\end{align*}
Uji kompetensi 1.5 nomor 2. Sebuah silinder pejal 2R dengan R adalah jari-jari. Pada bagian atasnya dibuat lubang membentuk setengah lingkaran dan lubang bagian bawahnya membentuk kerucut Tentukan letak titik beratnya diukur dari bidang alas. Alas kerucut berimpit dengan alas silinder.
Penyelesaian Fisika:
Kami yakin soal ini ada kekeliruan ketik, seharusnya berbunyi: Sebuah silinder pejal setinggi 2R dengan R adalah jari-jari. Pada bagian atasnya dibuat lubang membentuk setengah lingkaran bola dan lubang bagian bawahnya membentuk kerucut Tentukan letak titik beratnya diukur dari bidang alas. Alas kerucut berimpit dengan alas silinder.
Kita gambarkan soalnya...
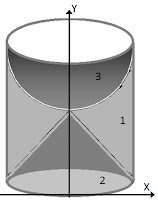
a. Kita bagi benda, menjadi TIGA; Anggap slinder pejal utuh sebagai bagian 1, kerucut bagian 2 dan setengah bola sebagai bagian 3.
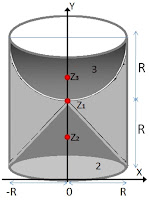
b. Kita hitung volume masing-masing bagian; \begin{align*} V_1&=\pi r^2t\\V_1&=\pi R^2(2R)=2\pi R^3\\\\V_2&=-\frac{1}{3}\pi r^2t\\V_2&=-\frac{1}{3}\pi R^2(R)=-\frac{1}{3}\pi R^3\\\\V_3&=-(\frac{1}{2})\frac{4}{3}\pi R^3=-\frac{2}{3}\pi R^3\end{align*}c. Kita cari koordinat titik berat masing-masing;
Lanjut ke Uji kompetensi 1.5 nomor 3 dan 4
\begin{align*}A_1&=\frac{1}{2}\pi R^{2}\\A_2&=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\\A_3&=-\frac{1}{2}\pi \left ( \frac{1}{2}R \right )^{2}=-\frac{1}{8}\pi R^{2}\end{align*}c. Kita cari koordinat titik berat masing-masing; \begin{align*}X_1&=R;\\ Y_1&=\frac{4R}{3\pi}\\X_2&=\frac{1}{2} R\\Y_2&=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\\X_3&=\frac{3}{2} R\\Y_3&=\frac{4(\frac{1}{2}R)}{3\pi}=\frac{2R}{3\pi}\end{align*}d. Hitung Xo dan Yo,
Untuk sumbu x atau $X_o$;\[\small \begin{align*}X_o&=\frac{A_1.X_1+A_2.X_2+A_3.X_3}{A_1+A_2+A_3} \\X_o&=\frac{\frac{1}{2}\pi R^2(R) -\frac{1}{8}\pi R^2(\frac{R}{2})-\frac{1}{8}\pi R^2(\frac{3R}{2 })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\X_o&=\frac{4(R) -(\frac{R}{2 })-(\frac{3R}{2 })}{2}=\frac{4R}{4}\\X_o&=R\end{align*}\]
Untuk sumbu y atau $Y_o$;\[\small \begin{align*}Y_o&=\frac{A_1.Y_1+A_2.Y_2+A_3.Y_3}{A_1+A_2+A_3} \\Y_o&=\frac{\frac{1}{2}\pi R^2(\frac{4R}{3\pi }) -\frac{1}{8}\pi R^2(\frac{2R}{3\pi })-\frac{1}{8}\pi R^2(\frac{2R}{3\pi })}{\frac{1}{2}\pi R^2-\frac{1}{8}\pi R^2-\frac{1}{8}\pi R^2} \\Y_o&=\frac{4(\frac{4R}{3\pi }) -(\frac{2R}{3\pi })-(\frac{2R}{3\pi })}{2}=\frac{12R}{6\pi}\\Y_o&=\frac{2R}{\pi}\end{align*}\]e. Tuliskan titik berat;\begin{align*}Z&=(R;\frac{2R}{\pi})\end{align*}
Uji kompetensi 1.5 nomor 2. Sebuah silinder pejal 2R dengan R adalah jari-jari. Pada bagian atasnya dibuat lubang membentuk setengah lingkaran dan lubang bagian bawahnya membentuk kerucut Tentukan letak titik beratnya diukur dari bidang alas. Alas kerucut berimpit dengan alas silinder.
Penyelesaian Fisika:
Kami yakin soal ini ada kekeliruan ketik, seharusnya berbunyi: Sebuah silinder pejal setinggi 2R dengan R adalah jari-jari. Pada bagian atasnya dibuat lubang membentuk setengah lingkaran bola dan lubang bagian bawahnya membentuk kerucut Tentukan letak titik beratnya diukur dari bidang alas. Alas kerucut berimpit dengan alas silinder.
Kita gambarkan soalnya...

a. Kita bagi benda, menjadi TIGA; Anggap slinder pejal utuh sebagai bagian 1, kerucut bagian 2 dan setengah bola sebagai bagian 3.
b. Kita hitung volume masing-masing bagian; \begin{align*} V_1&=\pi r^2t\\V_1&=\pi R^2(2R)=2\pi R^3\\\\V_2&=-\frac{1}{3}\pi r^2t\\V_2&=-\frac{1}{3}\pi R^2(R)=-\frac{1}{3}\pi R^3\\\\V_3&=-(\frac{1}{2})\frac{4}{3}\pi R^3=-\frac{2}{3}\pi R^3\end{align*}c. Kita cari koordinat titik berat masing-masing;

\[\small \begin{align*} Z_1&=(0,\left (\frac{1}{2} \right )t)\\Z_1&=(0,\left (\frac{1}{2} \right )2R)=(0,R)\\\\Z_2&=\left (0,\frac{1}{4}t \right )\\Z_2&=\left (0,\frac{1}{4}(R) \right )=\left (0,\frac{R}{4} \right )\\\\Z_3&=\left (0,(2R-\frac{3}{8}R)\right )=\left (0,\frac{13R}{8}\right )\end{align*}\] Hitung Xo dan Yo
Karena X ketiga benda =0, maka $X_o=0$; \[\small \begin{align*}Y_o&=\frac{V_1.Y_1+V_2.Y_2+V_3.Y_3}{V_1+V_2+V_3} \\Y_o&=\frac{2\pi R^3(R)-\frac{1}{3}\pi R^3(\frac{R}{4}) -\frac{2}{3}\pi R^3(\frac{13R}{8})}{2\pi R^3-\frac{1}{3}\pi R^3-\frac{2}{3}\pi R^3} \\Y_o&=\frac{R-(\frac{R}{24}) -(\frac{13R}{24})}{1-\frac{1}{6}-\frac{2}{6}}\\Y_o&=\frac{\frac{10R}{24}}{\frac{3}{6}}=\frac{5}{6}R\end{align*}\]e. Tuliskan titik berat;\begin{align*} Z=(0;\frac{5}{6}R)\end{align*}Lanjut ke Uji kompetensi 1.5 nomor 3 dan 4







