1. Nilai dari $\small \left (1-\frac{1}{2} \right )\left (1-\frac{1}{3} \right )\left (1-\frac{1}{4} \right ) \cdots \left (1-\frac{1}{2016} \right )$ adalah...
A. $\frac{1}{2011}$
B. $\frac{1}{2013}$
C. $\frac{1}{2015}$
D. $\frac{1}{2016}$
Penyelesaian: D
Nilai dari:
$\small \begin{align*}&\left (1-\frac{1}{2} \right )\left (1-\frac{1}{3} \right )\left (1-\frac{1}{4} \right )... \left (1-\frac{1}{2016} \right )\\&1-\frac{1}{2}=\frac{2}{2}-\frac{1}{2}=\frac{1}{2} \\&1-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}=\frac{2}{3} \\& 1-\frac{1}{4}=\frac{4}{4}-\frac{1}{4}=\frac{3}{4} \\&\textrm{maka:}\\&1-\frac{1}{2015}=\frac{2015}{2015}-\frac{1}{2015}=\frac{2014}{2015} \\&1-\frac{1}{2016}=\frac{2016}{2016}-\frac{1}{2016}=\frac{2015}{2016} \\&\textrm{sehingga;}\\&\left (1-\frac{1}{2} \right )\left (1-\frac{1}{3} \right )\left (1-\frac{1}{4} \right )... \left (1-\frac{1}{2016} \right )\\&=\frac{1}{2} \cdot \frac{2}{3} ... \frac{3}{4}\ \cdots \frac{2014}{2015} \cdot \frac{2015}{2016}\\&=\frac{1}{ 2} \cdot \frac{ 2}{ 3} \cdot \frac{ 3}{ 4}\frac{ 2014}{2015} ... \frac{ 2015}{2016}=\frac{1}{2016} \end{align*}$
2. Untuk setiap bilangan bulat positip $x,y$ didefenisikan $\small x \Delta y=\frac{xy}{y-x}$. Nilai $x$ yang memenuhi persamaan $\small (x \Delta 6)=4(x \Delta 3)$ adalah...
A. 9
B. 5
C. 4
D. 2
Penyelesaian: A
Dari persamaan $\small x \Delta y=\frac{xy}{y-x}$, maka ;
2. Untuk setiap bilangan bulat positip $x,y$ didefenisikan $\small x \Delta y=\frac{xy}{y-x}$. Nilai $x$ yang memenuhi persamaan $\small (x \Delta 6)=4(x \Delta 3)$ adalah...
A. 9
B. 5
C. 4
D. 2
Penyelesaian: A
Dari persamaan $\small x \Delta y=\frac{xy}{y-x}$, maka ;
$\small \begin{align*}
(x \Delta 6) & = 4(x \Delta 3) \\\frac{x \cdot 6}{6-x} & = 4 \left(\frac{x \cdot 3}{3-x} \right) \\\frac{6x}{6-x} & = 4 \left( \frac{3x}{3-x} \right) \\\frac{6x}{6-x} & = \frac{12x}{3-x}|_\text{dibagi 6x} \\\frac{1}{6-x} & = \frac{2}{3-x} \\3-x & = 2(6-x) \\3-x & = 12-2x \\-x+2x & = 12-3 \\x & = 9\end{align*}$
3. Suatu survei dilakukan pada siswa kelas X MIA SMA Unggul untuk mengetahui yang berminat mengikuti kegiatan Teater. Hasil survei ialah sebagai berikut: 25% dari total siswa putra dan 50% dari total siswa putri ternyata berminat mengikuti kegiatan tersebut; 90% dari total peminat kegiatan Teater ialah siswa putri. Rasio total siswa putri dan total siswa putra kelas X di sekolah tersebut adalah...
A. 9:1
B. 9:2
C. 9:3
D. 9:4
(x \Delta 6) & = 4(x \Delta 3) \\\frac{x \cdot 6}{6-x} & = 4 \left(\frac{x \cdot 3}{3-x} \right) \\\frac{6x}{6-x} & = 4 \left( \frac{3x}{3-x} \right) \\\frac{6x}{6-x} & = \frac{12x}{3-x}|_\text{dibagi 6x} \\\frac{1}{6-x} & = \frac{2}{3-x} \\3-x & = 2(6-x) \\3-x & = 12-2x \\-x+2x & = 12-3 \\x & = 9\end{align*}$
3. Suatu survei dilakukan pada siswa kelas X MIA SMA Unggul untuk mengetahui yang berminat mengikuti kegiatan Teater. Hasil survei ialah sebagai berikut: 25% dari total siswa putra dan 50% dari total siswa putri ternyata berminat mengikuti kegiatan tersebut; 90% dari total peminat kegiatan Teater ialah siswa putri. Rasio total siswa putri dan total siswa putra kelas X di sekolah tersebut adalah...
A. 9:1
B. 9:2
C. 9:3
D. 9:4
Penyelesaian: B
Misalkan jumlah total Putra = X dan Putri = Y. Yang berminat mengikuti teater ialah:
Misalkan jumlah total Putra = X dan Putri = Y. Yang berminat mengikuti teater ialah:
- 25% dari total siswa putra = 0,25X
- 50% dari total siswa putri = 0,5Y
- Total yang mengikuti teater ialah 0,25X+0,5Y.
- 90% dari total peminat kegiatan Teater ialah siswa putri, maka: $\small 0,9(0,25X+0,5Y)=0,5Y $ sehingga:
$\small \begin{align*}&0,9 \left( 0,25 X+0,5 Y \right) = 0,5 Y \\&0,25 X+0,5 Y = \frac{0,5 Y}{0,9} \\&0,25 X+0,5 Y = \frac{5}{9} Y \\&0,25 X = \frac{5}{9} Y - 0,5 Y \\&0,25 X = \frac{10}{18} Y - \frac{9}{18} Y \\&0,25 X = \frac{1}{18} Y \\&\frac{X}{4} = \frac{Y}{18} \\&\frac{Y}{X} = \frac{18}{4}=\frac{9}{2} \\&\end{align*}$
4. Perhatikan pola berikut:
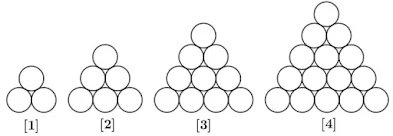
Banyak lingkaran pada pola ke-50 adalah...
A. 1275
B. 1326
C. 1452
D. 1546
Penyelesaian: B
Berdasarkan gambar, banyak lingkaran untuk tiap pola adalah:
- pola-1; 1+2=3; setara S2 deret aritmatika dengan a=1; b=1; n=2
- pola-2; 1+2+3=6; setara S3 deret aritmatika dengan a=1; b=1; n=3
- pola-4; 15=1+2+3+4+5; setara S5 deret aritmatika dengan a=1; b=1; n=5
- Dengan melihat aturan pola tersebut mengikuti aturan deret aritmatika maka banyak lingkaran pola ke-50 sama dengan S51 pada deret aritmatika dengan a=1; b=1; n=51;
$\small \begin{align*}S_{n} &= \frac{n}{2} \left( 2a +(n-1)b \right) \\S_{51} &= \frac{51}{2} \left( 2(1) +(51-1)1 \right) \\&= \frac{51}{2} \left( 2 +(50) \right) \\&= \frac{51}{2} (52) \\&= 1326\end{align*}$
5. Banyak angka $\small 17^{2}$ muncul pada akar persamaan :$\small \sqrt{17^{2}+17^{2}+ \cdots+17^{2}}=17^{2}+17^{2}+17^{2}$ bernilai benar adalah...
A. 17
B. 289
C. 2601
D. 4913
Penyelesaian: C
$\small \sqrt{17^{2}+17^{2}+ \cdots +17^{2}}=17^{2}+17^{2}+17^{2}$ bernilai benar;
$\small \sqrt{17^{2}+17^{2}+ \cdots +17^{2}}=3 \times 17^{2}$
$\small \begin{align*}17^2+17^2+ \cdots +17^2&=\left( 3 \times 17^2 \right)^2\\ 17^2+17^2+ \cdots +17^2&= 9 \times 17^2 \times 17^2\\ 17^2+17^2+ \cdots +17^2&= 9 \times 17^2 \times 17^2\end{align*}$
maka:
$\small \begin{align*}\sqrt{17^{2}+17^{2}+ \cdots +17^{2}}&=17^{2}+17^{2}+17^{2}\\\sqrt9 \times 17^2 \times 17^2&=17^2+17^2+17^2\end{align*}$
$\small 17^{2}$ yang ada dalam akar ialah $\small 9 \times 17^{2}=2601$
5. Banyak angka $\small 17^{2}$ muncul pada akar persamaan :$\small \sqrt{17^{2}+17^{2}+ \cdots+17^{2}}=17^{2}+17^{2}+17^{2}$ bernilai benar adalah...
A. 17
B. 289
C. 2601
D. 4913
Penyelesaian: C
$\small \sqrt{17^{2}+17^{2}+ \cdots +17^{2}}=17^{2}+17^{2}+17^{2}$ bernilai benar;
$\small \sqrt{17^{2}+17^{2}+ \cdots +17^{2}}=3 \times 17^{2}$
$\small \begin{align*}17^2+17^2+ \cdots +17^2&=\left( 3 \times 17^2 \right)^2\\ 17^2+17^2+ \cdots +17^2&= 9 \times 17^2 \times 17^2\\ 17^2+17^2+ \cdots +17^2&= 9 \times 17^2 \times 17^2\end{align*}$
maka:
$\small \begin{align*}\sqrt{17^{2}+17^{2}+ \cdots +17^{2}}&=17^{2}+17^{2}+17^{2}\\\sqrt9 \times 17^2 \times 17^2&=17^2+17^2+17^2\end{align*}$
$\small 17^{2}$ yang ada dalam akar ialah $\small 9 \times 17^{2}=2601$
6. Jika $x=2+\frac{3}{2+\frac{3}{2+\frac{3}{2+\frac{3}{x}}}}$ maka nilai $x$ adalah...
A. 3
B. 4
C. 5
D. 6
Penyelesaian: A
Bentuk soal:
Penyelesaian: A
Bentuk soal:
$\small \begin{align*}x=2+\frac{3}{2+\frac{3}{2+\frac{3}{2+\frac{3}{x}}}}\\\textrm{setara dengan:}\\x=2+\frac{3}{x}\\ \textrm{kita ubah mejadi:}\\x^{2} = 2x+3 &\\x^{2} -2x -3 = 0 &\\(x+1)(x-3) = 0& \\x = -1\ \text{(tdk memenuhi)} \\x = 3&\end{align*}$
7. Banyaknya bilangan real yang memenuhi $x^{2017}+x^{2016}-x^{2015}=x^{2014}$ adalah...
A. 0
B. 1
B. 1
C. 2
D. 3
Penyelesaian: B
$\small \begin{align*} &x^{2017}+x^{2016}-x^{2015} =x^{2014} \\&x^{2017}+x^{2016}-x^{2015}-x^{2014} =0 \\&\left(x^{2017} -x^{2015} \right )+\left(x^{2016} -x^{2014} \right ) =0 \\&x^{2015} \left(x^{2}-1 \right )+x^{2014} \left(x^{2} -1 \right ) =0 \\&\left( x^{2015}+x^{2014} \right ) \left(x^{2} -1 \right ) =0 \\&x^{2014} \left( x +1 \right ) \left(x^{2} -1 \right ) =0 \\&x^{2014} (x+1)(x+1)(x-1) =0 \\&x=-1;\ x=0;\ x =1\end{align*}$
Penyelesaian: B
$\small \begin{align*} &x^{2017}+x^{2016}-x^{2015} =x^{2014} \\&x^{2017}+x^{2016}-x^{2015}-x^{2014} =0 \\&\left(x^{2017} -x^{2015} \right )+\left(x^{2016} -x^{2014} \right ) =0 \\&x^{2015} \left(x^{2}-1 \right )+x^{2014} \left(x^{2} -1 \right ) =0 \\&\left( x^{2015}+x^{2014} \right ) \left(x^{2} -1 \right ) =0 \\&x^{2014} \left( x +1 \right ) \left(x^{2} -1 \right ) =0 \\&x^{2014} (x+1)(x+1)(x-1) =0 \\&x=-1;\ x=0;\ x =1\end{align*}$
8. A mampu merampungkan sendiri sebuah pekerjaan dalam waktu 2 jam, sedangkan B mampu merampungkan pekerjaan yang sama dalam waktu 6 jam. Jika mereka berdua bekerja bersama-sama, maka lama pekerjaan itu mampu selesai ialah ... jam
A. 1
B. $\frac{3}{2}$
C. 3
D. 4$\frac{1}{2}$
Penyelesaian: B
Misalkan:
9. Diketahui sistem persamaan:
$\small \begin{align*}&3a+7b+c = 315 \\&4a+10b+c = 420\end{align*}$
Penyelesaian: B
Misalkan:
- waktu A = $\small t_A$ dan waktu B = $\small t_B$
- waktu A dan B bersama-sama:
$\small \begin{align*}\frac{1}{t} & =\frac{1}{t_A}+\frac{1}{t_B}\\\frac{1}{t} &=\frac{1}{2}+\frac{1}{6} \\\frac{1}{t} & =\frac{3}{6}+\frac{1}{6} \\\frac{1}{t} & =\frac{4}{6} \\t&=\frac{6}{4}=\frac{3}{2}s\end{align*}$
9. Diketahui sistem persamaan:
$\small \begin{align*}&3a+7b+c = 315 \\&4a+10b+c = 420\end{align*}$
Maka nilai a+b+c adalah...
A. 100
A. 100
B. 105
C. 110
D. 150
Penyelesaian: D
Persamaan II dikurang Persamaan I:
$\small \begin{align*}4a+10b+c &= 420...(\textrm{II}) \\3a+7b+c &= 315 ...(\textrm{I})(-)\\\hline a + 3b &= 105\end{align*}$
Penyelesaian: D
Persamaan II dikurang Persamaan I:
$\small \begin{align*}4a+10b+c &= 420...(\textrm{II}) \\3a+7b+c &= 315 ...(\textrm{I})(-)\\\hline a + 3b &= 105\end{align*}$
Dari persamaan (II) ;
$\small \begin{align*} 4a+10b+c = 420 \\3a+a+9b+b+c & =420 \\3(a+3b)+a+b+c & =420 \\3(105)+a+b+c & =420 \\a+b+c & =420-315 \\a+b+c & =105\end{align*}$
$\small \begin{align*} 4a+10b+c = 420 \\3a+a+9b+b+c & =420 \\3(a+3b)+a+b+c & =420 \\3(105)+a+b+c & =420 \\a+b+c & =420-315 \\a+b+c & =105\end{align*}$
10. Diketahui f fungsi real yang memenuhi $\small f(x+f(x))=4f(x)$ dan $f(1)=4$. Maka nilai f(21) adalah...
A. 36
B. 48
C. 64
D. 72
Penyelesaian: C
Dari persamaan $\small f(x+f(x))=4f(x)$ dan $f(1)=4$ untuk $x=1$ maka:
Penyelesaian: C
Dari persamaan $\small f(x+f(x))=4f(x)$ dan $f(1)=4$ untuk $x=1$ maka:
$\small \begin{align*}
f(1+f(1)) & = 4f(1) \\f(1+4) & = 4 \cdot 4\\f(5) & = 16\end{align*}$
untuk $x=5$ maka:
$\small \begin{align*}f(5+f(5)) & = 4f(5) \\f(5+16) & = 4 \cdot 16\\f(21) & = 64\end{align*}$
f(1+f(1)) & = 4f(1) \\f(1+4) & = 4 \cdot 4\\f(5) & = 16\end{align*}$
untuk $x=5$ maka:
$\small \begin{align*}f(5+f(5)) & = 4f(5) \\f(5+16) & = 4 \cdot 16\\f(21) & = 64\end{align*}$








